Is Every Integer A Natural Number
News Leon
Apr 06, 2025 · 5 min read
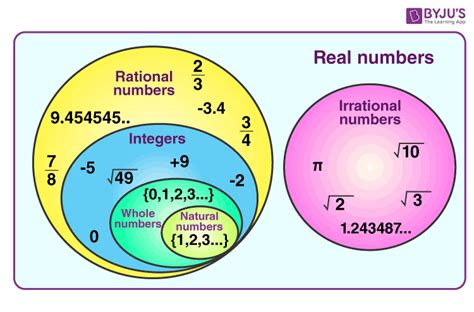
Table of Contents
Is Every Integer a Natural Number? Exploring the Relationship Between Number Sets
The question, "Is every integer a natural number?" seems deceptively simple. A quick glance might suggest a straightforward yes or no answer. However, a deeper dive into the definitions and properties of integers and natural numbers reveals a more nuanced relationship, one that hinges on the specific definition used for each set. This exploration will delve into the core concepts, exploring the similarities and crucial differences between these fundamental number systems and clarifying the subtle yet important distinctions.
Understanding Natural Numbers (Counting Numbers)
Natural numbers, often denoted by the symbol ℕ, are the most intuitive numbers we encounter. They are the numbers we use for counting: 1, 2, 3, 4, and so on. These numbers are used to quantify objects, events, or ideas. The fundamental characteristic of natural numbers is their positive and whole nature. There are no fractions, decimals, or negative values within this set.
Key Properties of Natural Numbers:
- Positive: All natural numbers are greater than zero.
- Whole: They are not fractions or decimals; they are complete units.
- Discrete: There are gaps between consecutive natural numbers; there's no number between 2 and 3, for example.
- Infinite: The set of natural numbers extends infinitely; there is no largest natural number.
Some definitions of natural numbers include zero (0). This is a point of contention amongst mathematicians, leading to two commonly used notations:
- ℕ₀ (or ℕ∪{0}): This notation includes zero, encompassing the set {0, 1, 2, 3, ...}.
- ℕ (or ℕ⁺): This notation excludes zero, encompassing only the set {1, 2, 3, ...}.
This subtle difference in definition has significant implications when considering the relationship between natural numbers and integers.
Delving into the Realm of Integers
Integers, denoted by the symbol ℤ, represent a broader set of numbers compared to natural numbers. The set of integers includes all whole numbers, both positive and negative, as well as zero. They can be visualized on a number line, extending infinitely in both positive and negative directions.
Key Properties of Integers:
- Positive, Negative, and Zero: Integers encompass positive numbers (1, 2, 3,...), negative numbers (-1, -2, -3,...), and zero (0).
- Whole: They are whole numbers, excluding fractions or decimals.
- Discrete: Similar to natural numbers, integers are discrete; there's no integer between 2 and 3, or between -1 and 0.
- Infinite: The set of integers extends infinitely in both the positive and negative directions.
Comparing Natural Numbers and Integers: A Venn Diagram Approach
To visualize the relationship between these number sets, a Venn diagram provides a clear representation:
If we consider the definition of natural numbers that excludes zero (ℕ⁺ = {1, 2, 3, ...}), the Venn diagram would show the set of natural numbers as a subset entirely contained within the set of integers. Every natural number is also an integer.
However, if we consider the definition of natural numbers that includes zero (ℕ₀ = {0, 1, 2, 3, ...}), the situation changes slightly. In this case, the set of natural numbers would still be largely contained within the set of integers, with only a small overlap, namely, only the non-negative integers will be in the set of natural numbers. This means that all the natural numbers are also integers, but not all integers are natural numbers.
Therefore, the answer to the question, "Is every integer a natural number?" is definitively no. There are many integers that are not natural numbers: all negative integers (-1, -2, -3, ...) are integers but not natural numbers, regardless of which definition of natural numbers you use.
Extending the Number System: Rational and Real Numbers
The number systems discussed so far – natural numbers and integers – are subsets of even larger number systems. Understanding their place within this broader hierarchy helps to further solidify the distinction between integers and natural numbers.
-
Rational Numbers (ℚ): Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. This set includes all integers, as an integer can be expressed as a fraction with a denominator of 1 (e.g., 3 = 3/1). It also includes fractions and terminating or repeating decimals.
-
Real Numbers (ℝ): Real numbers encompass all rational numbers and irrational numbers. Irrational numbers are numbers that cannot be expressed as a fraction of two integers (e.g., π, √2). Real numbers represent all points on the number line.
The hierarchy of number systems can be summarized as follows:
ℕ⁺ ⊂ ℤ ⊂ ℚ ⊂ ℝ
or
ℕ₀ ⊂ ℤ ⊂ ℚ ⊂ ℝ
where "⊂" denotes a proper subset (meaning one set is entirely contained within the other, but they are not identical).
Practical Applications and Implications
The distinction between integers and natural numbers might seem like a purely mathematical nicety, but understanding these differences has implications in various fields:
-
Computer Science: Many programming languages have different data types for integers and natural numbers (or unsigned integers), influencing memory allocation and arithmetic operations. Understanding the limitations of each data type is crucial for developing efficient and error-free software.
-
Physics and Engineering: In physics and engineering, the choice between using integers or natural numbers can depend on the context. For instance, when dealing with quantities that can't be negative (like the number of particles), natural numbers might be appropriate, while situations involving positive and negative values (like temperature or charge) require the use of integers.
-
Financial Modeling: In financial modeling, integers are frequently used to represent quantities like the number of shares or bonds, while natural numbers might be used to represent discrete quantities like years or periods.
-
Mathematics: This difference is fundamental to many mathematical proofs and theorems.
Conclusion: A Clear Distinction
In conclusion, while the set of natural numbers (whether including zero or not) forms a significant portion of the integers, not every integer is a natural number. The negative integers stand as a clear demarcation. Recognizing this distinction is fundamental to a solid understanding of number theory and its numerous applications across various scientific and technological domains. The seemingly simple question regarding the relationship between natural numbers and integers opens a door to a deeper appreciation of the richness and complexity of mathematical systems. The careful consideration of definitions and the implications of those definitions underscores the importance of precision and rigorous thinking in mathematics and its applications.
Latest Posts
Latest Posts
-
Observe The Number Line And Answer The Questions
Apr 07, 2025
-
What Does Mcg Mean In Measurement
Apr 07, 2025
-
How Many Yards In Quarter Mile
Apr 07, 2025
-
A Device That Directly Converts Solar Energy Into Electricity
Apr 07, 2025
-
What Is The Prime Number Between 20 And 30
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Is Every Integer A Natural Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.