Integrated Rate Law For Zero Order Reaction
News Leon
Mar 29, 2025 · 7 min read
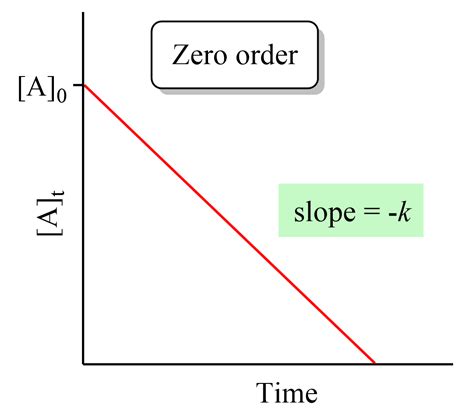
Table of Contents
Integrated Rate Law for Zero-Order Reactions: A Comprehensive Guide
Understanding reaction kinetics is fundamental in chemistry, providing insights into reaction mechanisms and predicting the behavior of chemical systems over time. A crucial aspect of this understanding involves the integrated rate laws, which mathematically describe the concentration of reactants as a function of time. This article delves into the integrated rate law for zero-order reactions, explaining its derivation, applications, and implications. We'll explore its practical use, common misconceptions, and how it differs from first and second-order reactions.
What is a Zero-Order Reaction?
A zero-order reaction is one whose rate is independent of the concentration of the reactant(s). This seemingly counterintuitive behavior arises from specific reaction mechanisms where factors other than reactant concentration control the reaction speed. Imagine a reaction where the rate is limited by something outside the reaction itself, such as the availability of a catalyst, the intensity of light, or the surface area of a solid reactant. In these cases, increasing the concentration of reactants won't speed up the reaction.
Key Characteristics of Zero-Order Reactions:
- Rate is constant: The rate of the reaction remains constant regardless of the concentration of the reactants.
- Rate is independent of reactant concentration: Doubling, tripling, or even halving the concentration of the reactants has no effect on the reaction rate.
- Reaction rate = k: The rate of the reaction is solely determined by the rate constant, k.
- Units of k: The rate constant, k, has units of concentration/time (e.g., mol L⁻¹ s⁻¹). This contrasts with first-order reactions (s⁻¹) and second-order reactions (L mol⁻¹ s⁻¹).
Deriving the Integrated Rate Law for Zero-Order Reactions
Let's consider a generic zero-order reaction:
A → Products
The rate of this reaction can be expressed as:
Rate = -d[A]/dt = k
where:
[A]represents the concentration of reactant A.trepresents time.kis the rate constant. The negative sign indicates that the concentration of A is decreasing over time.
To obtain the integrated rate law, we need to integrate this differential equation:
∫d[A] = -k∫dt
Integrating both sides, we get:
[A] = -kt + [A]₀
where:
[A]is the concentration of A at time t.[A]₀is the initial concentration of A at time t = 0.
This equation is the integrated rate law for a zero-order reaction. It represents a linear relationship between the concentration of the reactant and time.
Graphical Representation and Half-Life
The integrated rate law, [A] = -kt + [A]₀, has the form of a straight line (y = mx + c), where:
y = [A]m = -k(the slope)x = tc = [A]₀(the y-intercept)
Therefore, plotting [A] against t will yield a straight line with a slope of -k and a y-intercept of [A]₀. This provides a convenient graphical method for determining the rate constant, k, and the initial concentration of the reactant.
The half-life (t₁/₂) of a reaction is the time it takes for the concentration of a reactant to decrease to half its initial value. For a zero-order reaction, we can determine the half-life by substituting [A] = [A]₀/2 into the integrated rate law:
[A]₀/2 = -kt₁/₂ + [A]₀
Solving for t₁/₂, we obtain:
t₁/₂ = [A]₀ / 2k
This shows that the half-life of a zero-order reaction is directly proportional to the initial concentration. Higher initial concentrations lead to longer half-lives. This is a key difference compared to first and second-order reactions, where the half-life is independent of or inversely proportional to the initial concentration, respectively.
Examples of Zero-Order Reactions
While less common than first-order reactions, several real-world processes can be approximated as zero-order reactions under specific conditions:
- Enzyme-catalyzed reactions at high substrate concentrations: When the concentration of the substrate is significantly higher than the concentration of the enzyme, the enzyme becomes saturated. Further increases in substrate concentration do not increase the reaction rate because all enzyme active sites are occupied. The rate becomes independent of substrate concentration, exhibiting zero-order kinetics.
- Gas-phase reactions on a catalyst surface: The rate of a heterogeneous catalytic reaction can be limited by the available surface area of the catalyst. If the surface is saturated with reactant molecules, adding more reactant gas will not increase the reaction rate, leading to zero-order kinetics.
- Photochemical reactions: The rate of a photochemical reaction, such as the decomposition of ozone in the upper atmosphere, depends on the intensity of light rather than the concentration of ozone (within a certain range). The light intensity acts as a limiting factor, making the reaction appear zero-order.
- Electrochemical reactions: Under certain conditions, electrochemical reactions can exhibit zero-order kinetics, where the rate is controlled by factors such as the current density rather than the concentration of reactants in the solution.
Distinguishing Zero-Order Reactions from Other Reaction Orders
It's crucial to distinguish zero-order reactions from other reaction orders. This is typically done through graphical analysis and examining the dependence of the reaction rate on reactant concentration.
| Reaction Order | Rate Law | Integrated Rate Law | Half-life | Graphical Analysis |
|---|---|---|---|---|
| Zero-Order | Rate = k | [A] = -kt + [A]₀ | t₁/₂ = [A]₀ / 2k | Plot [A] vs. t; straight line with slope -k |
| First-Order | Rate = k[A] | ln[A] = -kt + ln[A]₀ | t₁/₂ = ln2 / k | Plot ln[A] vs. t; straight line with slope -k |
| Second-Order | Rate = k[A]² | 1/[A] = kt + 1/[A]₀ | t₁/₂ = 1 / k[A]₀ | Plot 1/[A] vs. t; straight line with slope k |
By plotting the appropriate function of concentration against time and observing the linearity, the reaction order can be definitively determined. A non-linear plot indicates that the reaction doesn't follow the assumed order.
Applications and Significance of Zero-Order Kinetics
Understanding zero-order kinetics is critical in various fields:
- Pharmacokinetics: Determining drug metabolism and elimination rates. Some drugs are eliminated from the body at a zero-order rate, particularly at high doses where the metabolic pathways become saturated.
- Environmental chemistry: Modeling the degradation of pollutants in the environment. The rate of pollutant breakdown can sometimes follow zero-order kinetics, influenced by factors like sunlight or microbial activity.
- Chemical engineering: Designing and optimizing chemical reactors. Knowing the reaction order is crucial for designing efficient and effective reactors.
- Material science: Studying the decomposition or degradation of materials. Understanding the reaction order helps predict the lifespan and performance of materials.
Limitations and Considerations
While the zero-order model provides valuable insights, it's essential to remember its limitations:
- Idealized Model: Many reactions are only approximately zero-order over a limited concentration range. As reactant concentration decreases, the reaction might transition to a different order.
- Complex Reaction Mechanisms: Zero-order kinetics often emerge from complex mechanisms, implying underlying processes that influence the overall rate. The model might not reveal the complete mechanistic details.
- Temperature Dependence: The rate constant, k, for a zero-order reaction is still temperature-dependent, following the Arrhenius equation. This dependency must be considered for accurate predictions across varying temperatures.
Conclusion
The integrated rate law for zero-order reactions provides a powerful tool for understanding and predicting the behavior of reactions where the rate is independent of reactant concentration. By analyzing the graphical representation and determining the half-life, we can characterize the reaction kinetics and apply this knowledge to various practical applications. However, it’s vital to remember the limitations of this model and consider the complexities of real-world chemical systems. A thorough understanding of zero-order kinetics contributes significantly to advancements in diverse fields, from drug development to environmental remediation and chemical engineering.
Latest Posts
Latest Posts
-
During Meiosis Crossing Over Takes Place Between
Apr 01, 2025
-
If Supply And Demand Both Decrease
Apr 01, 2025
-
Which Of The Following Best Describes Climate
Apr 01, 2025
-
What Are The Parts Of A Solution
Apr 01, 2025
-
What Is The Value Of 3 4
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Integrated Rate Law For Zero Order Reaction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
