If Cde Is A Straight Angle
News Leon
Apr 06, 2025 · 5 min read
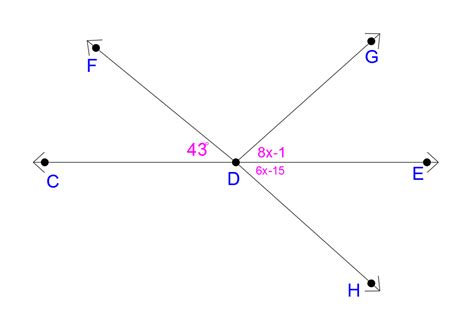
Table of Contents
If CDE is a Straight Angle: Exploring Geometric Implications and Problem Solving
If angle CDE is a straight angle, it immediately unlocks a wealth of geometric properties and problem-solving opportunities. Understanding this foundational concept is crucial for mastering geometry, trigonometry, and even more advanced mathematical fields. This comprehensive article will delve into the implications of a straight angle CDE, exploring its definition, properties, related theorems, and practical applications in various problem-solving scenarios.
Defining a Straight Angle
A straight angle is an angle that measures exactly 180 degrees. It's formed when two rays originate from a common point, extending in opposite directions to form a straight line. In the context of angle CDE being a straight angle, this means that points C, D, and E are collinear; they lie on the same straight line. This collinearity is a key characteristic that opens doors to numerous geometric deductions.
Visualizing Angle CDE
Imagine a straight line segment CE. Point D lies somewhere on this line segment. Angle CDE is formed by the rays CD and DE, which are essentially parts of the same straight line. Because they form a straight line, the measure of angle CDE is inherently 180°. This simple visualization helps solidify the fundamental concept.
Properties and Implications of a Straight Angle CDE
The fact that CDE is a straight angle has several significant consequences:
-
Linear Pair: If CDE is a straight angle, any two adjacent angles that form a linear pair with CDE will be supplementary. Supplementary angles are two angles whose measures add up to 180°. For instance, if angle CDI is adjacent to angle IDE, then ∠CDI + ∠IDE = 180°. This property is extensively used in solving geometric problems involving angles.
-
Collinearity: As previously mentioned, the points C, D, and E are collinear. This means they lie on the same straight line. This collinearity is a powerful tool in proving various geometric relationships and solving problems involving lines and segments.
-
Angle Relationships: If other angles are formed around point D, their relationship with angle CDE can be determined. For instance, vertically opposite angles formed by intersecting lines will be equal.
-
Applications in Trigonometry: Straight angles play a crucial role in trigonometry, particularly when dealing with angles greater than 180° or in the unit circle. Understanding straight angles is fundamental to understanding the periodic nature of trigonometric functions.
Problem Solving with a Straight Angle CDE
Let's explore various problem-solving scenarios that leverage the properties of a straight angle CDE:
Example 1: Finding Supplementary Angles
Suppose ∠CDI = 70°. Since ∠CDE is a straight angle (180°), and ∠CDI and ∠IDE form a linear pair, we can easily find the measure of ∠IDE:
∠IDE = 180° - ∠CDI = 180° - 70° = 110°
Example 2: Vertically Opposite Angles
Consider two intersecting lines forming angles around point D. If ∠CDI = 70°, then its vertically opposite angle, say ∠GDH, will also be 70°. Similarly, ∠IDE and its vertically opposite angle will be equal. This illustrates how the property of straight angles relates to vertically opposite angles.
Example 3: More Complex Angle Relationships
Imagine a transversal intersecting two parallel lines, creating angles around point D. If one of the angles formed at D is known, and angle CDE is a straight angle, we can determine all other angles formed by the intersection using the properties of parallel lines and the relationships between alternate interior, corresponding, and consecutive interior angles.
Example 4: Using Algebra
Consider a scenario where ∠CDI = 3x + 10° and ∠IDE = 5x - 20°. Since ∠CDE is a straight angle, we know:
∠CDI + ∠IDE = 180°
Substituting the given expressions:
(3x + 10°) + (5x - 20°) = 180°
Solving for x:
8x - 10° = 180° 8x = 190° x = 23.75°
Now we can find the measures of ∠CDI and ∠IDE by substituting the value of x back into the original expressions.
Example 5: Geometry Proofs
The property of a straight angle is frequently used in geometric proofs. Consider a proof that demonstrates the sum of angles in a triangle equals 180°. The proof often involves drawing a line parallel to one side of the triangle through a vertex, creating straight angles and applying angle relationships to demonstrate the sum.
Advanced Applications and Extensions
The concept of a straight angle extends beyond basic geometry. It forms the foundation for understanding:
-
Circular Geometry: In circular geometry, angles subtended by an arc on the circumference are related to the central angle subtended by the same arc. Understanding straight angles helps to derive relationships between these angles.
-
Coordinate Geometry: Straight angles are crucial in coordinate geometry, especially when determining the equation of a straight line or calculating distances and slopes.
Conclusion
Understanding that CDE is a straight angle opens up a vast array of possibilities in geometry and related fields. Its properties, including the creation of supplementary angles, collinearity, and relationships with other angles, allow for the solution of numerous complex geometric problems. Mastering this fundamental concept is essential for anyone seeking to excel in mathematics, laying the groundwork for more advanced concepts in geometry, trigonometry, and even calculus. Remember to practice solving problems using the properties of straight angles to solidify your understanding and develop your problem-solving skills. The more you practice, the more proficient you’ll become at identifying and utilizing the implications of a straight angle in various geometric contexts. The ability to readily recognize and apply these properties is a hallmark of a strong mathematical foundation.
Latest Posts
Latest Posts
-
Which Of The Following Pairs Is Correct
Apr 08, 2025
-
What Does After A Number Mean
Apr 08, 2025
-
How To Write A Letter For A Bank
Apr 08, 2025
-
Where Does Glycolysis Occur In A Prokaryotic Cell
Apr 08, 2025
-
What Is Iupac Name For The Compound Shown Below
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about If Cde Is A Straight Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.