How To Find Linear Mass Density
News Leon
Apr 03, 2025 · 6 min read
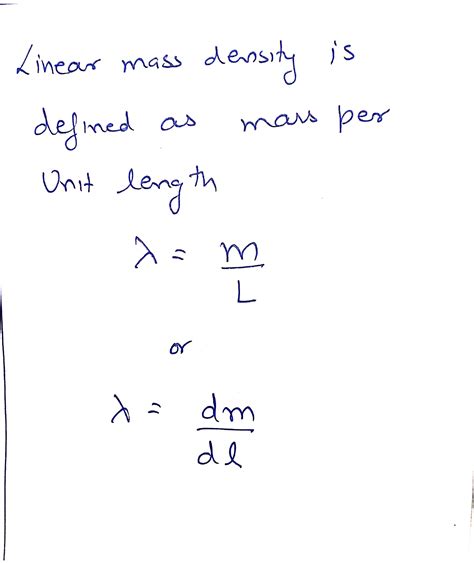
Table of Contents
How to Find Linear Mass Density: A Comprehensive Guide
Linear mass density, often represented by the Greek letter μ (mu), is a fundamental concept in physics and engineering. It describes the mass per unit length of a one-dimensional object, like a wire, rod, or string. Understanding how to calculate linear mass density is crucial for various applications, from analyzing the vibrational properties of strings in musical instruments to designing suspension systems in vehicles. This comprehensive guide will walk you through different methods of determining linear mass density, covering both theoretical calculations and practical measurements.
Understanding Linear Mass Density
Before diving into the methods, let's solidify our understanding of the concept itself. Linear mass density is simply the mass of an object divided by its length. This can be expressed mathematically as:
μ = m / L
where:
- μ represents linear mass density (usually in kg/m)
- m represents the mass of the object (usually in kg)
- L represents the length of the object (usually in m)
The units of linear mass density will vary depending on the units used for mass and length. Common units include kg/m, g/cm, and lb/ft. It's essential to maintain consistent units throughout your calculations to obtain accurate results.
Methods for Determining Linear Mass Density
There are several ways to find the linear mass density, depending on the information available and the nature of the object. Let's explore these methods in detail:
1. Direct Measurement: The Most Straightforward Approach
This is the most straightforward method, requiring only two measurements: mass and length.
Steps:
-
Measure the mass (m): Use a balance or scale to accurately measure the mass of the object. Ensure the object is stable and free from any external forces during the measurement. Record the mass in your chosen units (e.g., kilograms).
-
Measure the length (L): Use a ruler, measuring tape, or other appropriate measuring instrument to accurately determine the length of the object. Make sure to measure along the longest dimension of the object. Record the length in the same system of units as the mass (e.g., meters).
-
Calculate the linear mass density (μ): Divide the mass (m) by the length (L) to obtain the linear mass density.
μ = m / L
Example:
A wire has a mass of 10 grams and a length of 50 centimeters. To find its linear mass density:
-
Convert units to a consistent system: 10 g = 0.01 kg and 50 cm = 0.5 m
-
Apply the formula: μ = 0.01 kg / 0.5 m = 0.02 kg/m
Therefore, the linear mass density of the wire is 0.02 kg/m.
2. Indirect Measurement: When Direct Measurement is Difficult
Sometimes, direct measurement of mass or length might be challenging. For instance, you might have a very long wire or a complexly shaped object. In such cases, indirect methods are necessary.
a) Using a known length and a segment's mass:
If you can easily measure the mass of a segment of the object and you know the length of that segment, you can still calculate the linear mass density.
Steps:
-
Measure the mass (m<sub>segment</sub>) of a known length segment (L<sub>segment</sub>): This is typically easier than weighing the entire object.
-
Calculate the linear mass density (μ): Use the formula, substituting the segment's mass and length:
μ = m<sub>segment</sub> / L<sub>segment</sub>
This method assumes the linear mass density is uniform throughout the object.
b) Using density and cross-sectional area:
If you know the object's volume density (ρ) and its cross-sectional area (A), you can calculate the linear mass density. This is particularly useful for objects with uniform cross-sections.
Steps:
-
Determine the volume density (ρ): This might be found in material data tables or calculated from the mass and volume of a sample.
-
Measure the cross-sectional area (A): The method for this depends on the object's shape (e.g., πr² for a cylindrical wire).
-
Calculate the linear mass density (μ): The relationship is:
μ = ρ * A
This formula is derived from the fact that volume = area * length, and density = mass/volume.
3. Experimental Determination: Using Oscillations
This method is useful for determining the linear mass density of a string or wire by observing its vibrational properties. This relies on the relationship between the linear mass density, tension, and frequency of a vibrating string.
The relevant formula involves the fundamental frequency (f) of a vibrating string under tension (T):
f = (1/2L)√(T/μ)
Where:
- f is the fundamental frequency (Hz)
- L is the length of the string (m)
- T is the tension in the string (N)
- μ is the linear mass density (kg/m)
To determine μ using this method:
-
Measure the length (L) of the string.
-
Measure the tension (T) in the string. This might involve using a force gauge or by calculating the tension based on the weight attached to the string.
-
Measure the fundamental frequency (f) of the string. This can be done using a frequency meter or by comparing the sound to a known frequency.
-
Rearrange the formula to solve for μ:
μ = T / (4L²f²)
This method requires accurate measurements of frequency and tension and is most suitable for strings under relatively low tension.
Factors Affecting Accuracy
The accuracy of your linear mass density calculation depends on several factors:
- Accuracy of measurement tools: Using precise instruments is crucial. A high-quality balance and a calibrated ruler or measuring tape are essential for minimizing errors.
- Uniformity of the object: The methods assume a uniform mass distribution along the length. If the object is non-uniform, the calculated linear mass density will represent an average value.
- Environmental factors: Temperature and humidity can affect measurements, particularly for very sensitive measurements.
- Human error: Careful observation and accurate recording of measurements help to minimize human error.
Applications of Linear Mass Density
Understanding linear mass density is vital in numerous fields:
- Musical instrument design: The pitch of a stringed instrument is directly related to its linear mass density and tension.
- Civil engineering: In designing bridges and other structures, the linear mass density of cables and other components is crucial for calculating stress and strain.
- Mechanical engineering: The linear mass density of belts and chains affects their performance and lifespan.
- Physics experiments: Linear mass density is a key parameter in various physics experiments involving waves and oscillations.
- Material science: Analyzing the linear mass density can provide insights into the composition and properties of materials.
Conclusion
Determining linear mass density is a fundamental task in various scientific and engineering disciplines. While the direct measurement method is often the simplest, indirect methods offer solutions when direct measurement is impractical. Regardless of the method chosen, ensuring accurate measurements and understanding the limitations are key to obtaining reliable results. By mastering these techniques, you gain valuable insights into the properties of one-dimensional objects and their behavior under various conditions. Remember always to double-check your units and calculations to ensure accuracy and consistency in your findings.
Latest Posts
Latest Posts
-
What Is The Distance Between Saturn And The Sun
Apr 04, 2025
-
Example Of A Rational Number That Is Not An Integer
Apr 04, 2025
-
Select All Of The Following That Are Characteristics Of Heat
Apr 04, 2025
-
Which Of The Following Is Not True Of Dna
Apr 04, 2025
-
Any Computer Parts That You Can Actually Touch
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Find Linear Mass Density . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
