How Many Symmetry Lines Does A Square Have
News Leon
Apr 08, 2025 · 5 min read
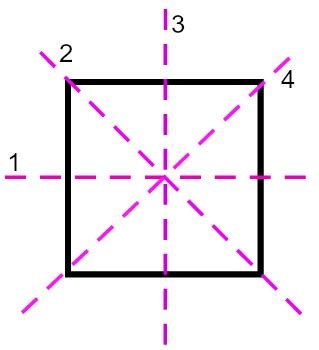
Table of Contents
How Many Lines of Symmetry Does a Square Have? A Comprehensive Exploration
Symmetry, a fundamental concept in mathematics and art, refers to a balanced and proportionate arrangement of elements. Understanding lines of symmetry is crucial in various fields, from geometry and design to crystallography and even architecture. This article delves into the fascinating world of symmetry, focusing specifically on the number of lines of symmetry a square possesses. We'll explore the definition of line symmetry, investigate different types of symmetry, and ultimately determine the precise number of lines of symmetry in a square, along with a detailed explanation of why.
Understanding Lines of Symmetry
A line of symmetry, also known as a reflectional symmetry or a mirror line, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along this line, both halves would perfectly overlap. The shape is said to be symmetrical about that line. Not all shapes possess lines of symmetry; some shapes may have multiple lines of symmetry, while others might not have any at all.
Types of Symmetry
Before diving into the specifics of a square, let's briefly explore other types of symmetry. While line symmetry is our primary focus, understanding other types provides a broader context:
1. Rotational Symmetry
Rotational symmetry occurs when a shape can be rotated about a central point (called the center of rotation) by a certain angle and still appear unchanged. The order of rotational symmetry is the number of times the shape looks identical during a 360-degree rotation. For example, a square has rotational symmetry of order 4 because it looks identical four times during a full rotation.
2. Translational Symmetry
This type of symmetry involves repeating a pattern along a straight line. You often see this in wallpapers, fabrics, and tessellations.
3. Point Symmetry (Central Symmetry)
A shape possesses point symmetry if it looks the same when rotated 180 degrees about a central point. This is also referred to as central symmetry.
Determining the Lines of Symmetry in a Square
Now, let's focus our attention on the square. A square is a regular quadrilateral with four equal sides and four right angles. Its inherent properties make it a prime example for studying lines of symmetry.
To determine the number of lines of symmetry in a square, we need to systematically investigate where we can draw lines that divide the square into two perfectly congruent halves.
Imagine a square ABCD, where A, B, C, and D are the vertices in clockwise order. We can draw lines of symmetry in two distinct ways:
1. Lines of Symmetry through Opposite Vertices
We can draw a line connecting two opposite vertices of the square. For example, a line connecting vertex A to vertex C is a line of symmetry. This line divides the square into two congruent triangles, mirroring each other. Similarly, a line connecting vertex B to vertex D is also a line of symmetry. This gives us two lines of symmetry.
2. Lines of Symmetry through Midpoints of Opposite Sides
We can also draw lines of symmetry by connecting the midpoints of opposite sides of the square. Let's consider the midpoint of side AB and the midpoint of side CD. A line connecting these midpoints is a line of symmetry. The same is true for the line connecting the midpoints of side BC and side AD. These are two more distinct lines of symmetry. This contributes another two lines of symmetry.
The Final Count: Four Lines of Symmetry
By combining the lines of symmetry through opposite vertices and the lines of symmetry through midpoints of opposite sides, we arrive at a total of four lines of symmetry in a square. These four lines of symmetry demonstrate the high degree of symmetry inherent in this geometric shape.
Symmetry in Different Contexts
The concept of lines of symmetry extends far beyond the realm of pure mathematics. Understanding symmetry is vital in several disciplines:
1. Art and Design
Artists and designers use symmetry extensively to create aesthetically pleasing and balanced compositions. From symmetrical paintings to architectural designs, symmetry contributes to visual harmony and elegance.
2. Nature
Symmetry is prevalent in the natural world. Many natural forms, such as snowflakes, flowers, and insects, exhibit striking symmetry, reflecting underlying patterns and processes in nature.
3. Science and Engineering
Symmetry plays a significant role in physics, chemistry, and engineering. Understanding symmetry helps scientists analyze and predict the behavior of molecules, crystals, and other structures.
4. Computer Graphics and Animation
Symmetry is crucial in computer-generated imagery (CGI) and animation, facilitating the creation of realistic and aesthetically appealing 3D models and animations.
Beyond the Square: Lines of Symmetry in Other Shapes
While we've focused on the square, let's briefly consider the lines of symmetry in other common shapes:
-
Equilateral Triangle: An equilateral triangle has three lines of symmetry. Each line connects a vertex to the midpoint of the opposite side.
-
Rectangle: A rectangle has two lines of symmetry. These lines connect the midpoints of opposite sides.
-
Circle: A circle has infinite lines of symmetry because any diameter of the circle is a line of symmetry.
Conclusion: The Significance of Symmetry
The investigation into the number of lines of symmetry a square possesses highlights the importance of understanding symmetry in diverse areas. The four lines of symmetry in a square aren't just a mathematical curiosity; they reflect an underlying order and balance that has implications across numerous fields, from artistic creation to scientific analysis. Understanding symmetry, therefore, provides a deeper appreciation of the world around us, whether it's the elegance of a snowflake or the precision of an engineered structure. The square, with its four lines of symmetry, serves as a perfect starting point to explore this fascinating concept.
Latest Posts
Latest Posts
-
Is Carbon Dioxide A Covalent Bond
Apr 08, 2025
-
What Happens When A Star Exhausts Its Core Hydrogen Supply
Apr 08, 2025
-
Find The Value Of X In A Kite
Apr 08, 2025
-
Which Of The Following Is True Regarding The Sarcoplasmic Reticulum
Apr 08, 2025
-
Draw Significant Resonance Structures For The Following Compound
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How Many Symmetry Lines Does A Square Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.