How Many Radians Is 60 Degrees
News Leon
Apr 08, 2025 · 5 min read
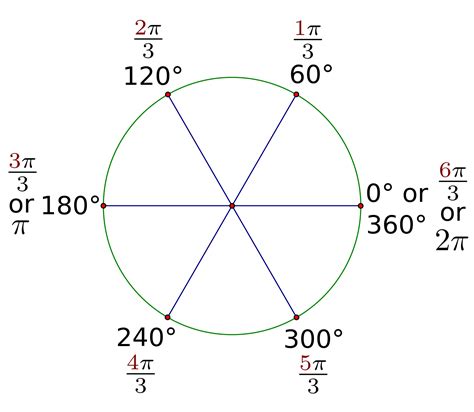
Table of Contents
How Many Radians is 60 Degrees? A Comprehensive Guide to Angle Conversions
Understanding the relationship between degrees and radians is crucial in various fields, from mathematics and physics to engineering and computer graphics. While degrees are the more familiar unit for measuring angles in everyday life, radians are the preferred unit in many advanced applications because of their inherent connection to the circle's radius and their simplification of many mathematical formulas. This article will delve deep into the conversion between degrees and radians, focusing specifically on converting 60 degrees to radians, and explore the underlying concepts.
Understanding Degrees and Radians
Before diving into the conversion, let's refresh our understanding of both units:
Degrees: A Familiar Measurement
Degrees are a unit of angular measurement where a full circle is divided into 360 equal parts. Each part represents one degree (1°). This system, while intuitive and widely used, lacks a direct mathematical connection to the circle's geometry. This is where radians come in.
Radians: A Mathematically Elegant System
Radians are another unit of angular measurement, defined by the ratio of the arc length to the radius of a circle. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. This definition directly links the angle to the fundamental geometric properties of the circle.
A full circle, which has a circumference of 2πr (where 'r' is the radius), subtends an angle of 2π radians. This makes radians a more natural unit in many mathematical contexts, especially in calculus and trigonometry.
The Conversion Factor: Bridging Degrees and Radians
The fundamental relationship between degrees and radians is:
180 degrees = π radians
This equation is the key to converting between the two systems. We can derive two crucial conversion factors from this:
- Radians to Degrees: Multiply the angle in radians by (180/π)
- Degrees to Radians: Multiply the angle in degrees by (π/180)
Converting 60 Degrees to Radians: A Step-by-Step Guide
Now, let's apply this knowledge to convert 60 degrees to radians. We'll use the degrees-to-radians conversion factor:
-
Start with the angle in degrees: 60°
-
Multiply by the conversion factor: 60° * (π/180)
-
Simplify the fraction: The 60 and 180 simplify to 1 and 3 respectively. This gives us: (π/3)
Therefore, 60 degrees is equal to π/3 radians.
Why Radians are Preferred in Advanced Mathematics and Physics
The inherent connection of radians to the circle's geometry leads to several advantages in advanced mathematical and scientific calculations:
-
Simplified Trigonometric Identities: Many trigonometric identities and formulas become significantly simpler when expressed in radians. For example, the derivative of sin(x) is cos(x) only if x is measured in radians. In degrees, you need an additional conversion factor.
-
Taylor Series Expansions: Taylor series expansions, which are fundamental tools in approximating functions, have simpler forms when using radians. These simpler forms lead to easier calculations and more efficient computations.
-
Calculus: Radians simplify calculus greatly. The derivative and integral formulas for trigonometric functions are much more elegant when working in radians.
-
Physics: In physics, especially in areas like rotational motion, angular velocity, and angular acceleration, radians are the preferred unit. This eliminates the need for cumbersome conversion factors and leads to more direct and meaningful interpretations of physical quantities.
Practical Applications: Where You'll Encounter Radian Measure
The use of radians extends far beyond theoretical mathematics. Here are some practical applications where you're likely to encounter radian measure:
-
Circular Motion: Calculating angular velocity, angular acceleration, and centripetal force in physics invariably involves radians.
-
Oscillations and Waves: Describing simple harmonic motion and wave phenomena often utilizes radian measure to represent the phase of the oscillation.
-
Computer Graphics and Animation: Generating smooth curves and rotations in computer graphics and animation often uses radians as the fundamental unit for angle representation. Game development relies heavily on this.
-
Signal Processing: Analyzing and manipulating signals in fields like audio engineering and telecommunications often employs radians to represent the phase of the signal.
-
Engineering: Many engineering disciplines, from mechanical engineering to electrical engineering, use radians in various calculations, especially those involving rotations and oscillations.
Beyond 60 Degrees: Mastering Angle Conversions
Understanding the conversion from 60 degrees to radians provides a solid foundation for converting any angle between degrees and radians. Remember the key conversion factors:
- Degrees to Radians: Multiply by π/180
- Radians to Degrees: Multiply by 180/π
Practice converting different angles, and you'll quickly master this essential skill. Experiment with converting angles like 30 degrees, 90 degrees, 180 degrees, 270 degrees and 360 degrees to reinforce your understanding. You’ll notice beautiful and predictable patterns.
Common Mistakes to Avoid When Converting Angles
While the conversion itself is straightforward, some common errors can lead to incorrect results. Here are some points to keep in mind:
-
Using the Wrong Conversion Factor: Always double-check whether you're using the correct factor (π/180 for degrees to radians, and 180/π for radians to degrees).
-
Incorrect Calculator Settings: Ensure your calculator is in radian mode when working with radians and in degree mode when working with degrees. Many errors arise from this simple oversight.
-
Approximating π Incorrectly: When performing calculations by hand, avoid rounding π prematurely. Retain as many decimal places as possible until the final step to minimize error accumulation. For most calculations, using π ≈ 3.14159 is sufficiently accurate.
Expanding Your Understanding: Further Exploration
Once you have a firm grasp on converting 60 degrees to radians and the underlying principles, you can explore more advanced topics, such as:
-
Trigonometric Functions in Radians: Deepen your understanding of trigonometric functions (sine, cosine, tangent) and their properties when the argument is in radians.
-
Unit Circle: Familiarize yourself with the unit circle and its importance in visualizing angles and their trigonometric values in radians.
-
Advanced Trigonometry and Calculus: Explore how radians simplify complex trigonometric identities and calculus problems.
By mastering the conversion between degrees and radians, you'll unlock a deeper understanding of mathematical and scientific concepts and improve your problem-solving capabilities in various fields. Remember that the seemingly simple conversion from 60 degrees to π/3 radians opens the door to a richer, more nuanced understanding of the mathematical world.
Latest Posts
Latest Posts
-
A Light Year Is A Measurement Of
Apr 08, 2025
-
A Mixture In Which The Composition Is Uniform Throughout
Apr 08, 2025
-
Is Carbon Dioxide A Covalent Bond
Apr 08, 2025
-
What Happens When A Star Exhausts Its Core Hydrogen Supply
Apr 08, 2025
-
Find The Value Of X In A Kite
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How Many Radians Is 60 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.