How Many Corners Does A Rectangular Pyramid Have
News Leon
Apr 05, 2025 · 5 min read
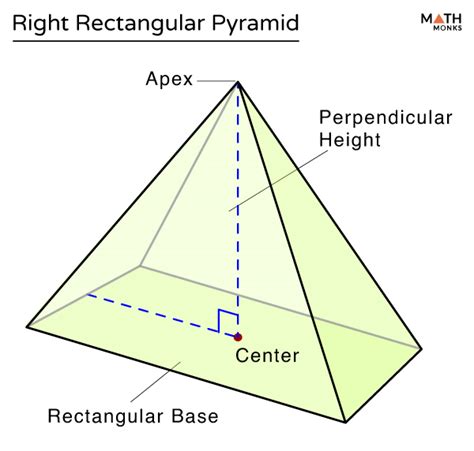
Table of Contents
How Many Corners Does a Rectangular Pyramid Have? A Deep Dive into Geometry
The seemingly simple question, "How many corners does a rectangular pyramid have?" opens a fascinating exploration into the world of geometry, specifically polyhedra. While the immediate answer might seem obvious, a closer examination reveals nuances and connections to broader mathematical concepts. This article will delve into not just the answer but also the underlying principles, related geometrical concepts, and even practical applications.
Understanding the Rectangular Pyramid
Before we count the corners, let's define what constitutes a rectangular pyramid. A rectangular pyramid is a three-dimensional geometric shape composed of:
- A rectangular base: This is the foundation of the pyramid, a four-sided polygon with four right angles.
- Four triangular faces: These faces connect each side of the rectangular base to a single apex point.
- One apex (vertex): This is the single point at the top of the pyramid where all four triangular faces meet.
Counting the Corners: The Straightforward Answer
A corner, in geometrical terms, is a vertex – a point where two or more edges meet. Therefore, a rectangular pyramid has a total of five corners. These are:
- Four corners at the base: These are the vertices of the rectangular base.
- One corner at the apex: This is the point where all four triangular faces converge.
Beyond the Simple Count: Exploring Related Concepts
While the answer itself is straightforward, understanding the underlying geometry is crucial for appreciating the complexity and elegance of this seemingly simple shape. Let's explore some related concepts:
1. Polyhedra and their Properties
A rectangular pyramid falls under the broader category of polyhedra. Polyhedra are three-dimensional shapes with flat polygonal faces. Understanding the properties of polyhedra, such as the Euler characteristic (V - E + F = 2, where V is vertices, E is edges, and F is faces), provides a powerful tool to verify the number of corners and other characteristics of a rectangular pyramid. Applying the Euler characteristic to our rectangular pyramid (5 vertices - 8 edges + 5 faces = 2) confirms the accuracy of our corner count.
2. Edges and Faces: A Complementary View
Understanding the number of edges and faces helps reinforce our understanding of the pyramid's structure. A rectangular pyramid has:
- 8 edges: Four edges form the rectangular base, and four more edges connect the base's corners to the apex.
- 5 faces: One rectangular base and four triangular faces.
The relationship between vertices, edges, and faces highlights the interconnectedness of geometrical properties. Any change in one element affects the others, underscoring the need for a systematic approach to geometrical analysis.
3. Regular vs. Irregular Rectangular Pyramids
It's important to distinguish between regular and irregular rectangular pyramids. In a regular rectangular pyramid, the base is a square, and the apex lies directly above the center of the base. This creates four congruent isosceles triangular faces. In an irregular rectangular pyramid, the base is a rectangle (not a square), and the apex's position can vary, resulting in four non-congruent triangular faces. However, the number of corners remains the same (five) regardless of the pyramid's regularity.
4. Applications in Real-World Contexts
Rectangular pyramids, although seemingly abstract geometrical constructs, appear in various real-world applications:
- Architecture: Pyramid shapes are often employed in architectural designs, from ancient Egyptian pyramids to modern buildings. Understanding the geometrical properties, including the number of corners, is vital for structural integrity and design considerations.
- Engineering: The principles of rectangular pyramids are used in various engineering projects, including the design of roofs, bridges, and other structures. Precise calculations based on geometrical understanding ensure stability and efficiency.
- Packaging: Some packaging designs utilize pyramid shapes for optimizing space and ensuring product stability during transport.
- Game Design: The shape and properties are used in various video games and 3D modeling applications.
Expanding the Discussion: Beyond Rectangular Pyramids
While we focused on rectangular pyramids, the concept of corners extends to other geometrical shapes. Let's briefly consider related polyhedra:
- Triangular Pyramids (Tetrahedra): These pyramids have a triangular base and three triangular faces, resulting in a total of four corners.
- Pentagonal Pyramids: With a pentagonal base and five triangular faces, these pyramids have six corners.
- General Pyramids: The number of corners in any pyramid is always one more than the number of sides of the base polygon.
This pattern reveals a fundamental relationship between the base polygon and the total number of vertices in the pyramid.
Practical Exercises and Further Exploration
To solidify your understanding, consider the following exercises:
- Draw a rectangular pyramid: Sketch a rectangular pyramid, clearly labeling its vertices, edges, and faces. Count the corners and verify your result using the Euler characteristic.
- Construct a 3D model: Building a physical model of a rectangular pyramid can significantly enhance your understanding of its geometrical properties.
- Explore other polyhedra: Investigate the properties of other polyhedra, such as cubes, octahedra, and dodecahedra, focusing on the relationship between vertices, edges, and faces.
Conclusion: The Significance of Geometric Understanding
The seemingly simple question about the number of corners in a rectangular pyramid opens a gateway to a deeper appreciation of geometry. By understanding the underlying principles, related concepts, and real-world applications, we gain a more comprehensive grasp of this fundamental mathematical field. The exploration goes beyond simply counting corners; it involves a systematic analysis of geometrical properties and their interconnections, highlighting the elegance and practicality of mathematical concepts. The five corners of a rectangular pyramid are not just points in space; they represent the intersection of lines and planes, the foundations of a solid geometrical structure with widespread practical applications.
Latest Posts
Latest Posts
-
Why Are Maps Important To Geographers
Apr 06, 2025
-
Google Search Console Crawl Reports Let You Monitor
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How Many Corners Does A Rectangular Pyramid Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
