Half Of A Number Decreased By 8 Is - 3
News Leon
Apr 13, 2025 · 4 min read
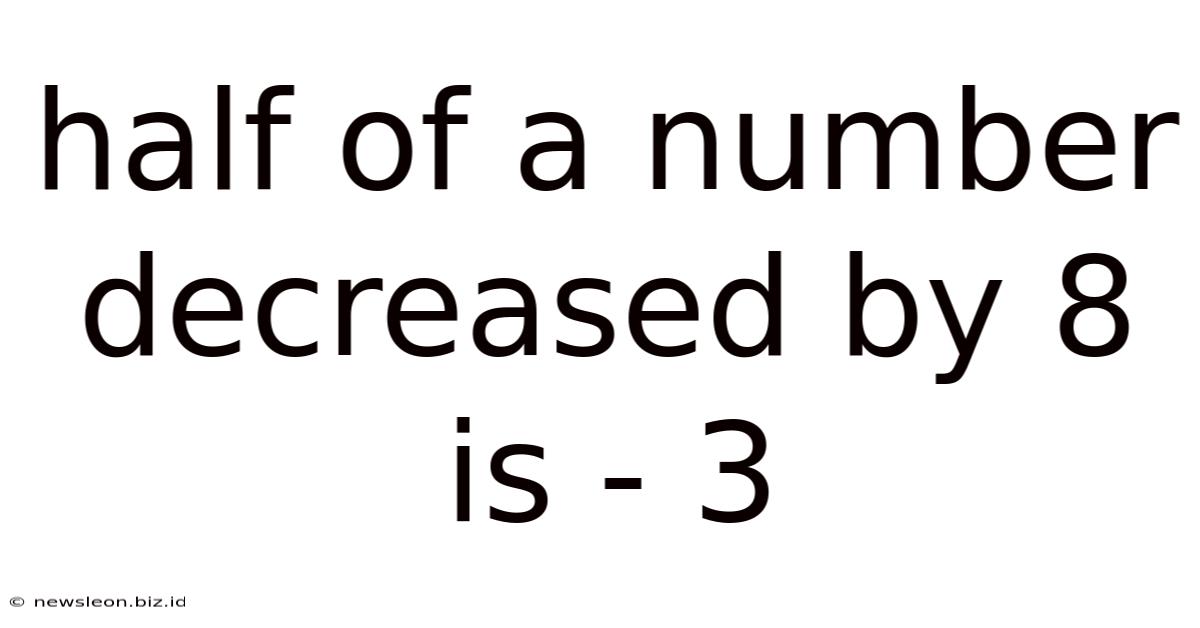
Table of Contents
Half of a Number Decreased by 8 is -3: A Comprehensive Exploration of Equation Solving
This seemingly simple mathematical statement, "half of a number decreased by 8 is -3," opens a door to a world of algebraic problem-solving techniques. This article will not only solve this specific problem but will also delve deep into the underlying concepts, explore various solution methods, and provide practical examples to solidify your understanding. We will also examine the importance of translating word problems into algebraic equations and highlight the significance of checking your solutions.
Understanding the Problem: From Words to Equations
The statement "half of a number decreased by 8 is -3" is a word problem. The first crucial step in solving such problems is translating the words into a mathematical equation. Let's break it down step-by-step:
- "a number": This represents an unknown value, which we typically denote with a variable, such as x.
- "half of a number": This translates to (1/2)x or x/2.
- "decreased by 8": This means subtracting 8 from the previous expression, giving us (x/2) - 8.
- "is -3": This indicates that the entire expression is equal to -3.
Therefore, the complete algebraic equation becomes:
(x/2) - 8 = -3
Solving the Equation: Multiple Approaches
Now that we have our equation, we can use various algebraic techniques to solve for x. Let's explore a few methods:
Method 1: Adding and Multiplying
This is a straightforward approach involving two simple steps:
-
Add 8 to both sides: This isolates the term with x. (x/2) - 8 + 8 = -3 + 8 (x/2) = 5
-
Multiply both sides by 2: This solves for x. 2 * (x/2) = 5 * 2 x = 10
Method 2: Clearing the Fraction First
Some prefer to eliminate fractions early in the process. This is achieved by multiplying the entire equation by the denominator (which is 2 in this case):
-
Multiply both sides by 2: 2 * [(x/2) - 8] = 2 * (-3) x - 16 = -6
-
Add 16 to both sides: x - 16 + 16 = -6 + 16 x = 10
Both methods yield the same result: x = 10.
Verifying the Solution: A Crucial Step
It's imperative to verify your solution by substituting the value of x back into the original equation:
(10/2) - 8 = 5 - 8 = -3
Since the equation holds true, our solution, x = 10, is correct.
Expanding the Concept: Variations and Applications
While the problem "half of a number decreased by 8 is -3" provides a basic framework, let's explore variations and real-world applications to deepen our understanding:
Variation 1: Different Operations
Consider a similar problem but with different operations: "Twice a number increased by 5 is 11." This translates to the equation:
2x + 5 = 11
Solving this equation using similar techniques (subtracting 5 from both sides and then dividing by 2) gives us x = 3.
Variation 2: More Complex Equations
Let's consider a more complex scenario: "One-third of a number, decreased by 7, and then multiplied by 4, equals 8." This translates to:
4 * [(x/3) - 7] = 8
Solving this requires a step-by-step approach, first dividing both sides by 4, then adding 7, and finally multiplying by 3. This gives us x = 27.
Real-World Applications
These types of equations are used extensively in various fields:
-
Finance: Calculating interest, discounts, or profit margins. For example, "After a 20% discount, the price of a product is $80. What was the original price?" This can be represented as an equation and solved using algebraic techniques.
-
Physics: Solving for unknown variables in motion problems, such as calculating speed, distance, or time.
-
Engineering: Determining dimensions, forces, or other physical quantities in designs.
-
Chemistry: Calculating concentrations, reaction rates, or other chemical properties.
Importance of Word Problem Solving
The ability to translate word problems into mathematical equations is a fundamental skill in mathematics and science. It's not just about finding the answer; it's about developing the ability to:
- Analyze information: Carefully examine the given information and identify the key components of the problem.
- Represent relationships: Translate the relationships between different quantities into mathematical expressions.
- Develop problem-solving strategies: Employ appropriate mathematical techniques to solve the equation.
- Verify solutions: Check the validity of the solution by substituting the value back into the original equation or problem statement.
Further Practice and Exploration
To enhance your understanding and skills, consider practicing various word problems of increasing complexity. You can find numerous resources online and in textbooks that offer a wide range of problems to tackle. Focus on understanding the underlying concepts and applying various solution methods.
Remember to always check your solutions! This crucial step not only confirms the accuracy of your calculations but also reinforces your understanding of the problem and its solution.
Conclusion: Mastering Algebraic Problem-Solving
The problem "half of a number decreased by 8 is -3," while seemingly simple, serves as a gateway to understanding and mastering algebraic problem-solving techniques. By carefully translating word problems into equations, applying appropriate algebraic methods, and verifying the solutions, you can confidently tackle more complex mathematical challenges in various fields. This skill is invaluable for success in mathematics, science, and numerous other disciplines. Remember to practice regularly and explore different problem types to solidify your understanding and build your confidence in algebraic manipulation.
Latest Posts
Related Post
Thank you for visiting our website which covers about Half Of A Number Decreased By 8 Is - 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.