Graph Of Y 4x X 2
News Leon
May 05, 2025 · 5 min read
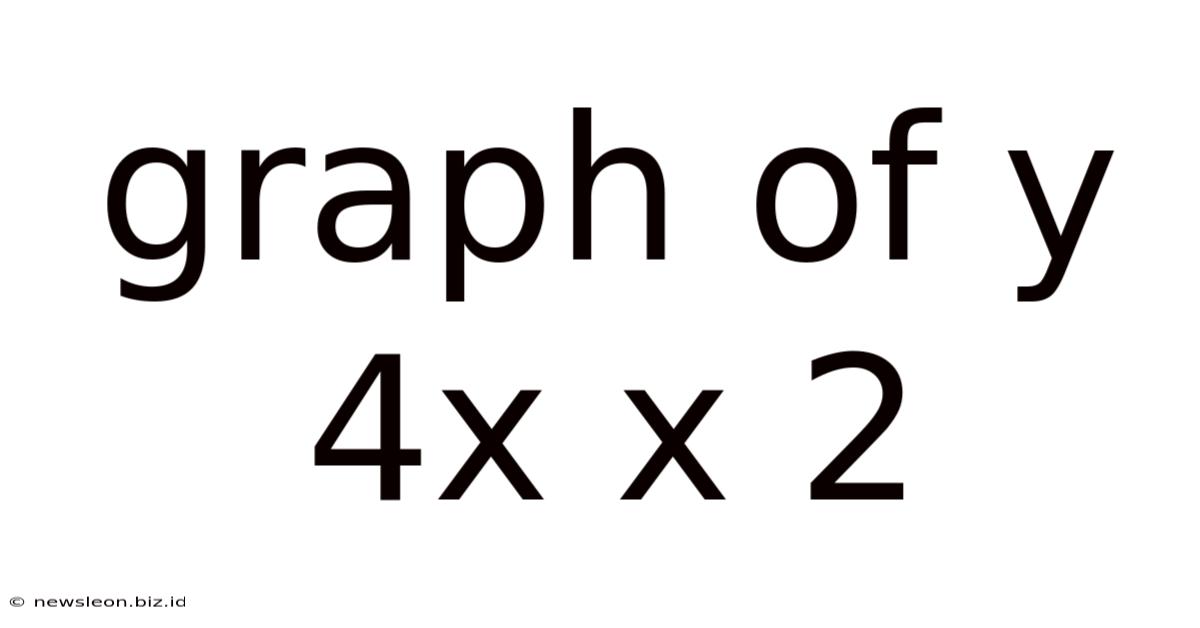
Table of Contents
Exploring the Graph of y = 4x - x²: A Comprehensive Analysis
The quadratic function y = 4x - x² represents a parabola, a fundamental shape in mathematics with numerous applications in physics, engineering, and other fields. This article delves into a comprehensive analysis of this specific parabola, exploring its key features, characteristics, and the methods used to understand its graphical representation. We'll cover everything from finding its vertex and intercepts to discussing its symmetry and practical interpretations.
Understanding the Basic Properties
Before diving into the specifics of y = 4x - x², let's refresh some fundamental concepts related to quadratic functions. A quadratic function is a polynomial function of degree two, generally expressed in the form y = ax² + bx + c, where 'a', 'b', and 'c' are constants and 'a' is not equal to zero. The graph of a quadratic function is always a parabola. The sign of 'a' determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
In our case, y = 4x - x², we can rewrite it in the standard form as y = -x² + 4x + 0. Here, a = -1, b = 4, and c = 0. Since 'a' is negative (-1), the parabola opens downwards. This immediately tells us about the general shape and direction of the curve.
Finding the Vertex: The Turning Point
The vertex of a parabola is the highest or lowest point on the curve, depending on whether the parabola opens upwards or downwards, respectively. For a parabola in the form y = ax² + bx + c, the x-coordinate of the vertex is given by the formula x = -b / 2a. The y-coordinate can then be found by substituting this x-value back into the original equation.
For y = -x² + 4x, we have a = -1 and b = 4. Therefore, the x-coordinate of the vertex is:
x = -4 / (2 * -1) = 2
Substituting x = 2 back into the equation:
y = -(2)² + 4(2) = -4 + 8 = 4
So, the vertex of the parabola is at the point (2, 4). This is the maximum point of the parabola since it opens downwards.
Determining the x-intercepts (Roots)
The x-intercepts, also known as the roots or zeros, are the points where the parabola intersects the x-axis (where y = 0). To find them, we set y = 0 and solve the quadratic equation:
0 = -x² + 4x
We can factor out an x:
0 = x(-x + 4)
This gives us two solutions: x = 0 and x = 4. Therefore, the x-intercepts are at the points (0, 0) and (4, 0).
Finding the y-intercept
The y-intercept is the point where the parabola intersects the y-axis (where x = 0). To find it, we simply substitute x = 0 into the equation:
y = -(0)² + 4(0) = 0
So, the y-intercept is at the point (0, 0). Notice that this is the same as one of the x-intercepts, indicating that the parabola passes through the origin.
Axis of Symmetry
The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves. For a parabola in the form y = ax² + bx + c, the equation of the axis of symmetry is given by x = -b / 2a. This is the same formula we used to find the x-coordinate of the vertex.
Therefore, the axis of symmetry for y = -x² + 4x is x = 2.
Analyzing the Concavity and Rate of Change
Since the coefficient of the x² term (a) is negative (-1), the parabola opens downwards, indicating a concave down shape. This means the function is initially increasing, reaches a maximum at the vertex, and then decreases.
The rate of change of the function, represented by its derivative, is given by:
dy/dx = 4 - 2x
This shows that the rate of change is positive when x < 2 (the function is increasing) and negative when x > 2 (the function is decreasing). At x = 2 (the vertex), the rate of change is zero.
Sketching the Graph
Now that we have all the key features – vertex, intercepts, axis of symmetry, and concavity – we can accurately sketch the graph of y = 4x - x². The parabola opens downwards, with its vertex at (2, 4). It intersects the x-axis at (0, 0) and (4, 0), and the y-axis at (0, 0). The axis of symmetry is the vertical line x = 2.
Applications and Real-World Examples
Quadratic functions, and parabolas in particular, have a wide range of applications in various fields:
-
Projectile Motion: The trajectory of a projectile under the influence of gravity is often modeled using a quadratic function. The maximum height reached by the projectile corresponds to the vertex of the parabola.
-
Optimization Problems: Quadratic functions are frequently used to model optimization problems, such as finding the maximum area of a rectangle given a fixed perimeter or maximizing profit given certain constraints. The vertex of the parabola represents the optimal solution.
-
Engineering Design: Parabolas are used in the design of bridges, arches, and other structures due to their inherent strength and stability.
-
Signal Processing: Quadratic functions are used in signal processing for tasks such as filtering and smoothing signals.
Further Exploration: Transformations and Comparisons
We can further explore the graph by comparing it to the basic parabola y = x² and understanding the effects of transformations. The equation y = 4x - x² can be seen as a transformation of y = x², involving a reflection about the x-axis, a horizontal shift, and a vertical shift. Analyzing these transformations provides a deeper understanding of the parabola's shape and position.
Conclusion: A Complete Picture of y = 4x - x²
This comprehensive analysis has provided a detailed understanding of the graph of y = 4x - x². By determining its vertex, intercepts, axis of symmetry, and concavity, we have been able to accurately describe its shape and behavior. Understanding these characteristics is crucial for applying quadratic functions to solve real-world problems and appreciate their significance in various fields. The parabola y = 4x - x², although seemingly simple, embodies the rich mathematical concepts underlying quadratic functions and their graphical representations. This analysis serves as a strong foundation for further exploration of more complex quadratic functions and their applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Graph Of Y 4x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.