Formula For Stored Energy In A Spring
News Leon
Apr 05, 2025 · 7 min read
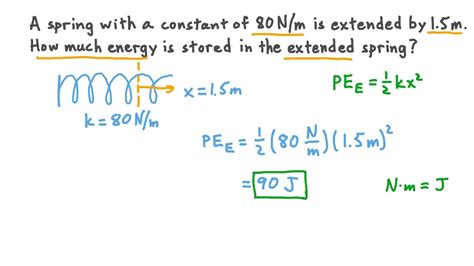
Table of Contents
- Formula For Stored Energy In A Spring
- Table of Contents
- The Formula for Stored Energy in a Spring: A Comprehensive Guide
- Understanding Hooke's Law: The Foundation of Spring Energy
- What is Spring Constant (k)?
- Deriving the Formula for Stored Energy in a Spring
- Understanding the Units
- Applications of the Spring Energy Formula
- 1. Mechanical Engineering:
- 2. Physics:
- 3. Automotive Industry:
- 4. Everyday Applications:
- Limitations of the Formula: Beyond Hooke's Law
- Factors Affecting Accuracy:
- Different Types of Springs and their Energy Storage
- Advanced Considerations: Beyond the Simple Formula
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
The Formula for Stored Energy in a Spring: A Comprehensive Guide
Understanding how springs store and release energy is fundamental to various fields, from mechanical engineering and physics to automotive design and even the creation of toys. This comprehensive guide delves deep into the formula for calculating the potential energy stored within a spring, exploring its derivation, applications, and limitations. We will also cover related concepts like Hooke's Law, spring constants, and different types of springs.
Understanding Hooke's Law: The Foundation of Spring Energy
The cornerstone of understanding stored energy in a spring is Hooke's Law. This law states that the force required to extend or compress a spring by some distance is directly proportional to that distance. Mathematically, it's expressed as:
F = -kx
Where:
- F represents the force applied to the spring (in Newtons).
- k is the spring constant (in Newtons per meter, N/m), a measure of the spring's stiffness. A higher k value indicates a stiffer spring requiring more force for the same displacement.
- x is the displacement from the spring's equilibrium position (in meters). The negative sign indicates that the force exerted by the spring opposes the displacement.
This seemingly simple equation is crucial because it lays the groundwork for calculating the potential energy stored in the spring.
What is Spring Constant (k)?
The spring constant, often denoted as 'k', is a critical parameter that defines a spring's behavior. It represents the resistance a spring offers to deformation. A higher spring constant indicates a stiffer spring, requiring more force to stretch or compress it a given distance. Conversely, a lower spring constant signifies a more flexible spring. The value of 'k' depends on several factors, including the material the spring is made of, its geometry (diameter of wire, number of coils, etc.), and the manufacturing process. Determining the spring constant often involves experimental methods such as measuring the force required to extend the spring by a known amount.
Deriving the Formula for Stored Energy in a Spring
To understand the formula for stored energy, we need to consider the work done in compressing or stretching the spring. Work (W) is defined as the integral of force (F) with respect to displacement (x):
W = ∫₀ˣ F dx
Substituting Hooke's Law (F = -kx) into the work integral, we get:
W = ∫₀ˣ (-kx) dx
Solving this integral gives:
W = -½kx²
Since the work done is stored as potential energy (PE) in the spring, the formula for the potential energy stored in a spring is:
PE = ½kx²
This equation tells us that the potential energy stored is directly proportional to the square of the displacement and the spring constant. This means that doubling the displacement quadruples the stored energy, highlighting the non-linear relationship between displacement and stored energy.
Understanding the Units
It's crucial to understand the units involved in the potential energy formula. The spring constant (k) is measured in Newtons per meter (N/m), and the displacement (x) is in meters (m). Therefore, the potential energy (PE) is measured in Joules (J), which is the standard unit of energy in the International System of Units (SI).
Applications of the Spring Energy Formula
The formula for stored energy in a spring has widespread applications in numerous fields:
1. Mechanical Engineering:
- Spring Design: Engineers use this formula to design springs for specific applications, ensuring they can store the required amount of energy without exceeding their elastic limit. This is crucial in designing suspension systems, shock absorbers, and other mechanical components.
- Energy Storage Systems: Springs can be used as simple energy storage devices. The formula helps engineers determine the size and stiffness of the springs needed to store a specific amount of energy.
2. Physics:
- Simple Harmonic Motion (SHM): The potential energy stored in a spring is essential for understanding SHM, a type of periodic motion where the restoring force is directly proportional to the displacement. The energy continually transforms between potential energy (stored in the spring) and kinetic energy (motion of the mass).
- Energy Conservation: The formula is vital in applying the principle of energy conservation, where the total energy of a system (potential + kinetic) remains constant.
3. Automotive Industry:
- Suspension Systems: Springs are integral parts of vehicle suspension systems. The formula helps in designing springs that provide the necessary comfort and handling characteristics.
- Shock Absorbers: Shock absorbers use springs to dampen vibrations and shocks, improving vehicle ride quality and safety. The formula is used in designing these systems to absorb the kinetic energy of impacts effectively.
4. Everyday Applications:
- Toys: Many toys, such as wind-up toys, utilize springs to store and release energy, resulting in the toy's motion.
- Door Closers: Spring-loaded door closers use the stored energy in a spring to automatically close doors.
Limitations of the Formula: Beyond Hooke's Law
It's crucial to understand that the formula PE = ½kx² is based on Hooke's Law, which is only valid within the elastic limit of the spring. Beyond this limit, the spring undergoes permanent deformation, and the linear relationship between force and displacement no longer holds. In such cases, the formula becomes inaccurate, and more complex models are needed to describe the spring's behavior.
Factors Affecting Accuracy:
- Material Properties: The formula assumes a perfectly elastic material. Real-world springs exhibit some degree of inelasticity, meaning some energy is lost as heat during deformation.
- Spring Geometry: The formula assumes an ideal spring geometry. Variations in coil diameter, pitch, and other geometric factors can affect the spring constant and the accuracy of the energy calculation.
- Temperature Effects: Temperature changes can alter the spring's stiffness, affecting the stored energy.
Different Types of Springs and their Energy Storage
The formula PE = ½kx² applies to various spring types, but the value of 'k' and the accuracy of the formula can vary depending on the spring's design:
- Helical Springs (Coil Springs): These are the most common type of springs and are well-described by Hooke's Law and the associated energy formula.
- Leaf Springs: Used in vehicle suspensions, these springs have a different geometry and their energy storage calculations are more complex.
- Torsion Springs: These springs store energy by twisting, and their energy calculation involves a different formula related to the torsional stiffness.
- Belleville Washers (Disc Springs): These springs have a non-linear force-displacement relationship, making the application of the ½kx² formula less accurate.
Advanced Considerations: Beyond the Simple Formula
While the simple formula PE = ½kx² provides a good approximation for many applications, more complex scenarios require advanced considerations:
- Non-linear Springs: Many real-world springs don't follow Hooke's Law perfectly. For such springs, the relationship between force and displacement is non-linear, and numerical methods or more advanced mathematical models are needed to calculate the stored energy.
- Dynamic Loading: When a spring is subjected to rapidly changing forces, its behavior becomes more complex due to inertia and damping effects. In such cases, dynamic analysis is required.
- Fatigue and Failure: Repeated loading and unloading of a spring can lead to fatigue and eventually failure. The formula for stored energy doesn't directly address these aspects, and fatigue analysis techniques are needed for reliable design.
Conclusion
The formula PE = ½kx² is a cornerstone in understanding the energy storage capabilities of springs. Its simplicity belies its wide-ranging applications across various disciplines. However, it's crucial to remember its limitations, particularly the reliance on Hooke's Law and the assumptions about ideal spring behavior. Understanding these limitations and applying more advanced techniques where necessary is vital for accurate and reliable design in engineering and scientific applications. This comprehensive guide has aimed to provide a solid foundation for understanding this important formula and its implications. By grasping the principles outlined here, you'll be better equipped to work with springs and leverage their energy storage potential in various contexts.
Latest Posts
Latest Posts
-
The Iupac Name For No2 Is
Apr 09, 2025
-
Protein Digestion Takes Place In The
Apr 09, 2025
-
What Is The Relation Between Momentum And Force
Apr 09, 2025
-
Which Of The Following Are True About The Brain
Apr 09, 2025
-
A Line Segment Has Two Endpoints True Or False
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Formula For Stored Energy In A Spring . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.