Formula For Orbital Velocity Of Satellite
News Leon
Apr 08, 2025 · 6 min read
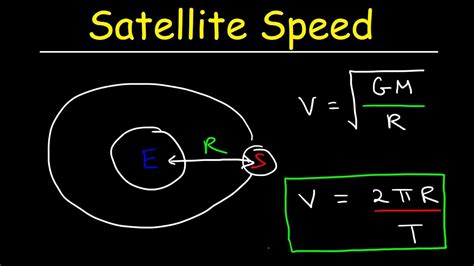
Table of Contents
The Formula for Orbital Velocity of a Satellite: A Deep Dive
Understanding the principles governing satellite motion is crucial for numerous applications, from global communication networks to precise GPS navigation. At the heart of this understanding lies the formula for orbital velocity, a calculation that determines the speed a satellite needs to maintain a stable orbit around a celestial body. This article provides a comprehensive exploration of this formula, delving into its derivation, the factors influencing it, and its practical implications.
Understanding Orbital Velocity
Orbital velocity is the speed required for an object to maintain a stable orbit around a larger celestial body. This speed is a delicate balance between the object's inertia (its tendency to move in a straight line) and the gravitational pull of the celestial body. If the object moves too slowly, gravity will pull it inwards, causing it to spiral down and potentially collide with the larger body. If it moves too fast, it will overcome the gravitational pull and escape into space.
The key to a stable orbit lies in the precise balance between these two forces. The object is constantly "falling" towards the larger body, but its tangential velocity (its velocity parallel to the surface of the body) ensures it continuously misses, resulting in a continuous, curved path – the orbit.
Deriving the Formula for Orbital Velocity
The formula for orbital velocity can be derived using Newtonian mechanics and the law of universal gravitation. Let's break down the derivation step-by-step:
-
Centripetal Force: For an object to move in a circular orbit, it must experience a centripetal force, directed towards the center of the orbit. This force is given by:
Fc = mv²/rwhere:
Fcis the centripetal forcemis the mass of the satellitevis the orbital velocityris the orbital radius (the distance between the satellite and the center of the celestial body)
-
Gravitational Force: The centripetal force required to keep the satellite in orbit is provided by the gravitational force between the satellite and the celestial body. This force is given by Newton's Law of Universal Gravitation:
Fg = GMm/r²where:
Fgis the gravitational forceGis the universal gravitational constant (approximately 6.674 x 10⁻¹¹ Nm²/kg²)Mis the mass of the celestial body (e.g., Earth, Mars)mis the mass of the satelliteris the orbital radius
-
Equating Forces: For a stable orbit, the centripetal force must equal the gravitational force:
Fc = Fgmv²/r = GMm/r² -
Solving for Orbital Velocity: We can now solve this equation for the orbital velocity (
v):v² = GM/rv = √(GM/r)This is the formula for the orbital velocity of a satellite in a circular orbit.
Factors Affecting Orbital Velocity
The formula highlights the key factors influencing a satellite's orbital velocity:
-
Mass of the Celestial Body (M): A larger celestial body (e.g., a more massive planet) exerts a stronger gravitational pull, requiring a higher orbital velocity to maintain a stable orbit at a given radius.
-
Orbital Radius (r): The distance from the center of the celestial body to the satellite significantly affects orbital velocity. A smaller orbital radius implies a stronger gravitational pull, necessitating a higher orbital velocity. Conversely, a larger orbital radius means a weaker gravitational pull, allowing for a lower orbital velocity. This inverse square root relationship is crucial to understand.
-
Universal Gravitational Constant (G): This constant is a fundamental constant in physics and remains unchanged. It represents the strength of gravitational interaction between any two objects with mass.
Applications of the Orbital Velocity Formula
The formula for orbital velocity has wide-ranging applications in various fields:
-
Satellite Deployment: This formula is crucial for accurately calculating the velocity needed to launch a satellite into a specific orbit. Incorrect velocity calculations can lead to the satellite either falling back to Earth or escaping into space.
-
GPS Navigation: Global Positioning System (GPS) satellites rely on precise orbital calculations to provide accurate location data. The formula for orbital velocity plays a pivotal role in ensuring the satellites maintain their designated orbits.
-
Geostationary Satellites: Geostationary satellites appear stationary above a specific point on Earth's equator. This requires a specific orbital velocity and radius, which are calculated using the orbital velocity formula. These satellites are crucial for communication, weather forecasting, and other applications requiring constant observation of a specific geographical location.
-
Space Exploration: Planning interplanetary missions and accurately calculating trajectories requires a thorough understanding of orbital mechanics and the orbital velocity formula. This allows for precise maneuvers and fuel efficiency during space travel.
-
Orbital Maneuvers: Changes in a satellite's orbit, such as raising or lowering its altitude, require careful adjustments to its velocity. The orbital velocity formula provides the basis for calculating the necessary velocity changes to achieve these maneuvers.
Beyond Circular Orbits: Elliptical Orbits
The formula derived above applies specifically to circular orbits. However, most satellite orbits are elliptical, meaning the distance between the satellite and the celestial body varies throughout the orbit. For elliptical orbits, the orbital velocity is not constant but varies depending on the satellite's position in its orbit.
At the point of closest approach to the celestial body (perigee), the satellite experiences the strongest gravitational pull and thus has the highest orbital velocity. Conversely, at the point furthest from the celestial body (apogee), the gravitational pull is weakest, resulting in the lowest orbital velocity. The calculation of orbital velocity for elliptical orbits involves more complex equations involving Kepler's Laws of Planetary Motion.
Considering Other Factors: Atmospheric Drag and Perturbations
While the basic formula provides a good approximation, it simplifies several real-world factors.
-
Atmospheric Drag: Satellites orbiting within the Earth's atmosphere experience atmospheric drag, which gradually reduces their orbital velocity. This drag is more significant for lower-altitude orbits and needs to be accounted for in precise orbital calculations.
-
Gravitational Perturbations: The gravitational pull of other celestial bodies, such as the Sun and Moon, can cause slight perturbations in a satellite's orbit. These perturbations need to be factored into long-term orbital predictions.
-
Non-Spherical Celestial Bodies: The assumption of a perfectly spherical celestial body is an oversimplification. The Earth, for instance, is slightly oblate (bulges at the equator), introducing variations in gravitational pull depending on latitude. This leads to precession and other orbital effects.
Conclusion: The Importance of Orbital Velocity Calculations
The formula for orbital velocity, while seemingly simple, represents a fundamental principle in celestial mechanics. It is a critical tool for numerous applications, from satellite deployment and GPS navigation to space exploration and understanding the dynamics of planetary systems. Understanding the factors influencing orbital velocity and the limitations of simplified models allows for more accurate predictions and efficient management of spacecraft and satellite operations. Future advancements in space technology will continue to rely heavily on a refined and comprehensive understanding of orbital mechanics, building upon the foundation provided by this fundamental formula. The accuracy and precision of orbital calculations directly impact the success and longevity of space-based missions, reinforcing the enduring importance of this key equation in our exploration and utilization of space.
Latest Posts
Latest Posts
-
The Principal Cation In Intracellular Fluid Is
Apr 08, 2025
-
Having Two Identical Alleles For A Trait
Apr 08, 2025
-
Is Grain Farming Commercial Or Subsistence
Apr 08, 2025
-
Composed Mostly Of Carbon Hydrogen And Oxygen
Apr 08, 2025
-
What Fraction Is Represented By Point A
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Formula For Orbital Velocity Of Satellite . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.