Find X So That L Is Parallel To M
News Leon
Apr 03, 2025 · 6 min read
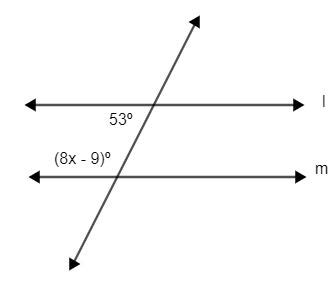
Table of Contents
Find x so that l is parallel to m: A Comprehensive Guide
Finding the value of 'x' that makes lines 'l' and 'm' parallel involves understanding several geometric concepts and applying them strategically. This guide delves into various scenarios, providing a step-by-step approach to solving these types of problems. We'll explore different methods and provide ample examples to solidify your understanding.
Understanding Parallel Lines and Transversals
Before we dive into finding 'x', let's refresh our understanding of parallel lines and transversals. Parallel lines are lines that never intersect, no matter how far they are extended. A transversal is a line that intersects two or more other lines. When a transversal intersects parallel lines, specific angle relationships are created. These relationships are crucial for solving problems where we need to find 'x' to make lines parallel.
Key Angle Relationships
Several pairs of angles are formed when a transversal intersects two lines. Understanding these relationships is fundamental:
- Corresponding Angles: These are angles that are in the same relative position at an intersection when a line intersects two other lines. If the lines are parallel, corresponding angles are congruent (equal).
- Alternate Interior Angles: These angles are on opposite sides of the transversal and inside the two lines. If the lines are parallel, alternate interior angles are congruent.
- Alternate Exterior Angles: These angles are on opposite sides of the transversal and outside the two lines. If the lines are parallel, alternate exterior angles are congruent.
- Consecutive Interior Angles (Same-Side Interior Angles): These angles are on the same side of the transversal and inside the two lines. If the lines are parallel, consecutive interior angles are supplementary (add up to 180 degrees).
- Consecutive Exterior Angles (Same-Side Exterior Angles): These angles are on the same side of the transversal and outside the two lines. If the lines are parallel, consecutive exterior angles are supplementary.
Methods for Finding x
The specific method for finding 'x' depends on the given information in the problem. Let's explore some common scenarios:
1. Using Corresponding Angles
Scenario: You are given a diagram showing two lines intersected by a transversal. Several angles are labeled with algebraic expressions involving 'x'. At least one pair of corresponding angles is given.
Method: Set the expressions for the corresponding angles equal to each other and solve for 'x'.
Example:
Let's say angle 1 is 3x + 10 and angle 5 is 5x - 20. If angle 1 and angle 5 are corresponding angles, and lines l and m are parallel, then:
3x + 10 = 5x - 20
Solving for x:
2x = 30 x = 15
Therefore, if x = 15, lines l and m are parallel because the corresponding angles are congruent.
2. Using Alternate Interior Angles
Scenario: Similar to the corresponding angles scenario, but now we are working with alternate interior angles.
Method: Set the expressions for the alternate interior angles equal to each other and solve for 'x'.
Example:
Let's say angle 3 is 2x + 5 and angle 6 is 4x - 15. If angle 3 and angle 6 are alternate interior angles, and lines l and m are parallel, then:
2x + 5 = 4x - 15
Solving for x:
2x = 20 x = 10
Therefore, if x = 10, lines l and m are parallel because the alternate interior angles are congruent.
3. Using Alternate Exterior Angles
Scenario: Similar to the previous scenarios, but this time we're using alternate exterior angles.
Method: Set the expressions for the alternate exterior angles equal to each other and solve for 'x'.
Example:
Let's say angle 1 is 6x - 5 and angle 8 is 2x + 25. If angle 1 and angle 8 are alternate exterior angles, and lines l and m are parallel, then:
6x - 5 = 2x + 25
Solving for x:
4x = 30 x = 7.5
Therefore, if x = 7.5, lines l and m are parallel because the alternate exterior angles are congruent.
4. Using Consecutive Interior Angles
Scenario: This scenario involves consecutive interior angles. Remember, consecutive interior angles are supplementary when lines are parallel.
Method: Add the expressions for the consecutive interior angles and set their sum equal to 180 degrees. Solve for 'x'.
Example:
Let's say angle 3 is x + 20 and angle 5 is 2x + 40. If angle 3 and angle 5 are consecutive interior angles, and lines l and m are parallel, then:
(x + 20) + (2x + 40) = 180
Solving for x:
3x + 60 = 180 3x = 120 x = 40
Therefore, if x = 40, lines l and m are parallel because the consecutive interior angles are supplementary.
5. Using Consecutive Exterior Angles
Scenario: Similar to consecutive interior angles, but now we are using consecutive exterior angles.
Method: Add the expressions for the consecutive exterior angles and set their sum equal to 180 degrees. Solve for 'x'.
Example:
Let's say angle 1 is 3x - 10 and angle 8 is 2x + 30. If angle 1 and angle 8 are consecutive exterior angles, and lines l and m are parallel, then:
(3x - 10) + (2x + 30) = 180
Solving for x:
5x + 20 = 180 5x = 160 x = 32
Therefore, if x = 32, lines l and m are parallel because the consecutive exterior angles are supplementary.
Advanced Scenarios and Considerations
Some problems may present more complex scenarios:
- Multiple Transversals: Problems might involve more than one transversal intersecting the lines 'l' and 'm'. In such cases, you might need to use multiple angle relationships to find 'x'.
- Combined Angle Relationships: You may need to combine different angle relationships (e.g., using corresponding angles and then using the result to find consecutive interior angles).
- Indirect Relationships: Sometimes the relationship between angles and 'x' might not be direct. You might need to solve for another variable first before finding 'x'.
Practical Application and Real-World Examples
The concept of finding 'x' to make lines parallel has numerous practical applications in various fields:
- Construction: Ensuring parallel walls and beams in building construction relies heavily on understanding parallel lines and angle relationships.
- Engineering: Designing parallel tracks for trains or designing parallel components in machinery requires precise calculations using geometry.
- Cartography: Creating accurate maps involves understanding parallel lines of latitude and longitude.
- Computer-Aided Design (CAD): CAD software utilizes geometric principles to create precise parallel lines and shapes for various applications.
Conclusion
Finding 'x' to make lines 'l' and 'm' parallel involves a systematic application of geometric principles. By understanding the key angle relationships formed when a transversal intersects parallel lines, and by systematically solving equations, you can accurately determine the value of 'x' that ensures parallelism. Remember to carefully analyze the diagram, identify the relevant angle relationships, and use the appropriate method to solve for 'x'. Practice is key to mastering these techniques. With enough practice, you'll be able to confidently tackle even the most complex problems involving parallel lines. Remember to always check your work to ensure your solution makes sense within the context of the given diagram and angle relationships.
Latest Posts
Latest Posts
-
What Is The Prime Factorization Of 120
Apr 04, 2025
-
Do Nonmetals Gain Or Lose Electrons
Apr 04, 2025
-
Oxygen Released During Photosynthesis Comes From
Apr 04, 2025
-
Which Of The Following Defines A Coenzyme
Apr 04, 2025
-
When There Is A Decrease In Both Demand And Supply
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find X So That L Is Parallel To M . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
