Find The Value Of Log Root 625 Base 5
News Leon
May 04, 2025 · 5 min read
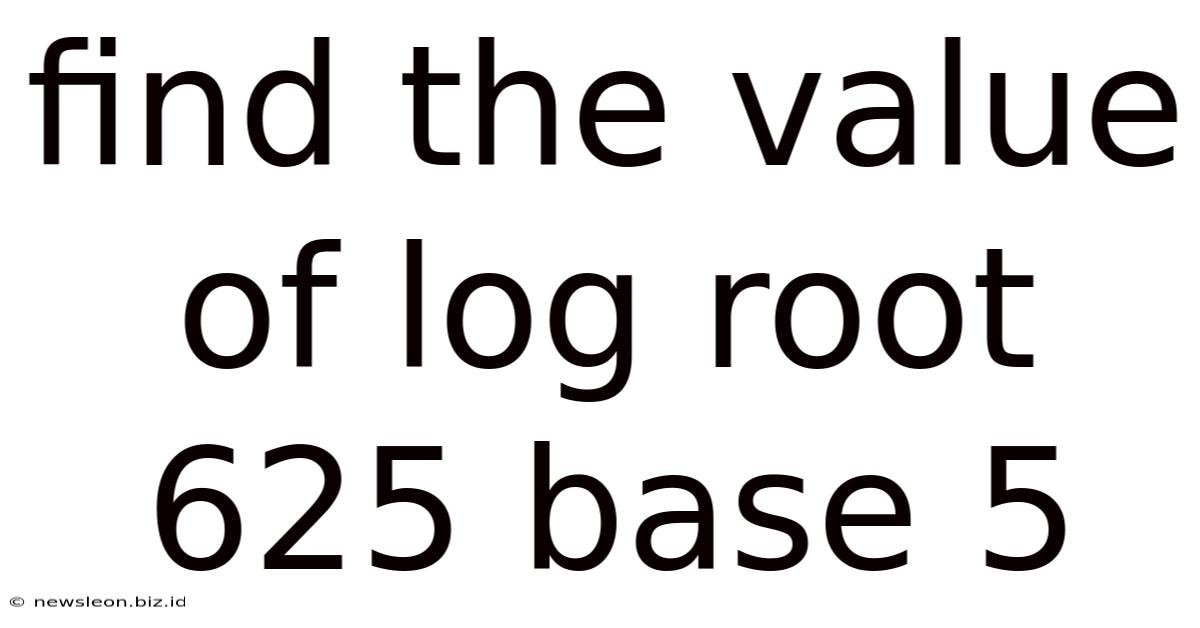
Table of Contents
Finding the Value of log√625 base 5: A Comprehensive Guide
This article delves into the detailed process of solving the logarithmic equation log√625₅, explaining the underlying concepts of logarithms and providing step-by-step calculations. We will explore various approaches to reach the solution, emphasizing the fundamental principles and offering insights into related logarithmic properties. Beyond the specific problem, this guide aims to equip you with a stronger understanding of logarithms and their applications.
Understanding Logarithms
Before tackling the problem directly, let's establish a solid foundation in logarithms. A logarithm is essentially the inverse operation of exponentiation. The expression logₐb = x means that aˣ = b, where:
- a is the base of the logarithm (must be positive and not equal to 1).
- b is the argument (must be positive).
- x is the exponent or the logarithm's value.
In simpler terms, the logarithm answers the question: "To what power must we raise the base (a) to get the argument (b)?"
For example, log₁₀100 = 2 because 10² = 100. Here, 10 is the base, 100 is the argument, and 2 is the logarithm's value.
Properties of Logarithms
Several key properties of logarithms simplify calculations and are crucial for solving more complex logarithmic equations. These properties include:
- Product Rule: logₐ(xy) = logₐx + logₐy
- Quotient Rule: logₐ(x/y) = logₐx - logₐy
- Power Rule: logₐ(xⁿ) = n logₐx
- Change of Base Rule: logₐx = (logₓx) / (logₓa) (Useful for changing the base to a more convenient one, often 10 or e)
- Logarithm of 1: logₐ1 = 0 (Since a⁰ = 1 for any a ≠ 0)
- Logarithm of the Base: logₐa = 1 (Since a¹ = a)
Understanding these properties is vital for efficiently solving logarithmic equations.
Solving log√625₅
Now, let's address the core problem: finding the value of log√625₅.
First, we need to understand what √625 represents. The square root of 625 is 25, since 25 * 25 = 625. Therefore, our equation becomes:
log₂₅₅
This simplifies our problem considerably. We are now looking for the exponent to which we must raise 5 to obtain 25.
We can write this as:
5ˣ = 25
It's evident that x = 2 because 5² = 25.
Therefore, log₂₅₅ = 2
Alternatively, we can use the power rule of logarithms. Recall that √625 can be written as 625^(1/2). Applying the power rule:
log₅(625^(1/2)) = (1/2) * log₅625
Now, we need to find the value of log₅625. This means finding the exponent x such that 5ˣ = 625. We can express 625 as a power of 5:
625 = 5⁴
Therefore, log₅625 = 4.
Substituting this back into our equation:
(1/2) * log₅625 = (1/2) * 4 = 2
Again, we arrive at the solution: log√625₅ = 2
Alternative Approaches and Verification
While the previous methods provide straightforward solutions, let's explore another approach using the change of base rule. We can change the base to 10 (common logarithm) or e (natural logarithm) for calculation using a calculator:
log√625₅ = (log₁₀√625) / (log₁₀5)
Using a calculator:
log₁₀√625 ≈ 1.39794 log₁₀5 ≈ 0.69897
Therefore:
(log₁₀√625) / (log₁₀5) ≈ 1.39794 / 0.69897 ≈ 2
This confirms our previous result. This approach is useful when dealing with logarithms that are not easily expressed as whole number exponents.
Expanding on Logarithmic Concepts: Applications and Further Exploration
The simple problem of finding log√625₅ provides a solid foundation for understanding more complex logarithmic applications. Logarithms are used extensively in various fields, including:
- Chemistry: Calculating pH values (logarithmic scale of acidity)
- Physics: Measuring sound intensity (decibels are logarithmic units) and earthquake magnitude (Richter scale).
- Computer Science: Analyzing algorithms' complexity and efficiency.
- Finance: Calculating compound interest and exponential growth.
- Mathematics: Solving exponential equations and simplifying complex expressions.
Exploring these applications will further solidify your understanding of the power and versatility of logarithms.
Beyond the Basics: Dealing with More Complex Logarithmic Equations
Let's consider more challenging scenarios to illustrate the application of logarithmic properties:
Example 1: Solve for x: log₂(x + 2) + log₂(x - 1) = 3
Using the product rule:
log₂[(x + 2)(x - 1)] = 3
This implies:
(x + 2)(x - 1) = 2³ = 8
Expanding and solving the quadratic equation:
x² + x - 2 = 8
x² + x - 10 = 0
Using the quadratic formula, we find two possible solutions for x. However, we must check if these solutions are valid within the context of the original logarithmic equation (arguments must be positive).
Example 2: Solve for x: log₃(2x - 1) = 2
This directly translates to:
3² = 2x - 1
9 = 2x - 1
10 = 2x
x = 5
Again, it is crucial to verify that the solution results in a positive argument for the logarithm.
These examples showcase how the fundamental properties of logarithms, learned from the initial problem, are applied to solve more complex equations. The key is to systematically apply the appropriate rules and always validate solutions by ensuring the arguments remain positive.
Conclusion: Mastering Logarithms for Enhanced Problem-Solving
The problem of finding the value of log√625₅, while seemingly simple, provides a stepping stone to understanding the fundamental principles of logarithms. By mastering these principles, including the essential properties, you'll be well-equipped to tackle more challenging logarithmic equations and appreciate their wide-ranging applications across diverse fields. Remember the importance of consistent practice and the use of verification to ensure accuracy in your solutions. Continuous learning and exploration of advanced concepts will solidify your mastery of logarithms and enhance your problem-solving capabilities in various mathematical and scientific contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Find The Value Of Log Root 625 Base 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.