Find The Height Of A Trapezium
News Leon
Apr 07, 2025 · 6 min read
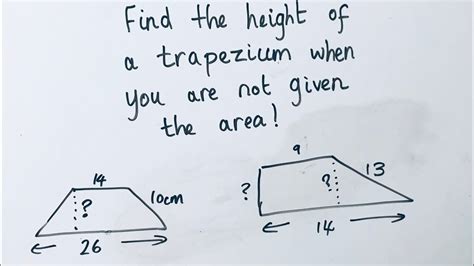
Table of Contents
Finding the Height of a Trapezium: A Comprehensive Guide
Finding the height of a trapezium (also known as a trapezoid) is a common problem in geometry, appearing in various mathematical contexts and real-world applications. This comprehensive guide will explore multiple methods for calculating the height, catering to different levels of mathematical understanding and providing practical examples to solidify your knowledge. We'll cover everything from simple cases with readily available information to more complex scenarios requiring the application of advanced geometric principles.
Understanding the Trapezium and its Height
Before diving into the calculation methods, let's establish a clear understanding of what a trapezium is and what its height represents. A trapezium is a quadrilateral with at least one pair of parallel sides. These parallel sides are called bases, often denoted as b₁ and b₂. The height (h) of a trapezium is the perpendicular distance between these two parallel bases. This height is crucial for calculating the area of the trapezium, a key application in various fields like architecture, surveying, and engineering.
Method 1: Using the Area and Base Lengths
This is perhaps the most straightforward method, provided you already know the area and the lengths of both bases. The formula for the area (A) of a trapezium is:
A = ½(b₁ + b₂)h
Where:
- A = Area of the trapezium
- b₁ = Length of the first base
- b₂ = Length of the second base
- h = Height of the trapezium
To find the height, we simply rearrange the formula:
h = 2A / (b₁ + b₂)
Example:
Let's say we have a trapezium with an area of 30 square units, a base length of 8 units (b₁), and a second base length of 4 units (b₂). Plugging these values into the formula, we get:
h = 2 * 30 / (8 + 4) = 60 / 12 = 5 units
Therefore, the height of the trapezium is 5 units.
Considerations for this method:
- This method is only applicable if the area and both base lengths are known.
- Accuracy depends heavily on the accuracy of the provided area and base lengths. Any error in these measurements will directly impact the calculated height.
Method 2: Using Trigonometry (Right-Angled Triangle Approach)
This method is useful when you have the lengths of one base and one of the non-parallel sides, along with an angle. We can create a right-angled triangle within the trapezium and use trigonometric functions (sine, cosine, tangent) to find the height.
Example:
Consider a trapezium where one base (b₁) is 10 units, one non-parallel side (s) is 6 units, and the angle between the non-parallel side and the base is 30°. We can draw a perpendicular line from one end of the shorter base to the longer base, creating a right-angled triangle. The height (h) is the side opposite the 30° angle in this right-angled triangle. Therefore, we can use the sine function:
sin(30°) = h / s
h = s * sin(30°) = 6 * sin(30°) = 6 * 0.5 = 3 units
Therefore, the height of the trapezium is 3 units.
Considerations for this method:
- This method requires knowledge of at least one angle and specific side lengths. The angle must be related to the height and a known side length.
- Trigonometric functions are necessary, requiring a calculator or understanding of trigonometric values.
Method 3: Dividing the Trapezium into Rectangles and Triangles
This method is particularly useful when dealing with irregular trapezia. The idea is to divide the trapezium into simpler shapes – rectangles and right-angled triangles – whose heights can be more easily calculated.
Example:
Imagine a trapezium with bases b₁ and b₂. Let's assume b₁ > b₂. We can extend the shorter base (b₂) to meet the extensions of the non-parallel sides, forming a rectangle with height h and width equal to b₂. This leaves two right-angled triangles on either side of the rectangle. The height of these triangles will also be h. By calculating the dimensions of these triangles (using Pythagorean theorem or other trigonometric methods) you can determine the height 'h'.
Considerations for this method:
- Requires careful geometrical construction and calculation of various dimensions.
- The process may involve multiple steps, increasing the potential for errors in calculation. Precise measurement is vital.
Method 4: Using Coordinate Geometry
If you have the coordinates of the four vertices of the trapezium, you can leverage coordinate geometry to find the height.
Example: Let's assume the vertices are A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), and D(x₄, y₄). If AB and CD are the parallel sides, then the height is the perpendicular distance between the lines containing AB and CD. This involves finding the equations of the lines containing AB and CD, then finding the distance between them using the formula for the distance between two parallel lines. This requires a strong understanding of analytical geometry, involving the calculation of slopes, intercepts, and the use of the distance formula.
Considerations for this method:
- Requires familiarity with coordinate geometry and its associated formulas.
- Can be computationally intensive, especially for complex coordinates.
Method 5: Using Heron's Formula (for Isosceles Trapezium)
If the trapezium is an isosceles trapezium (two non-parallel sides are equal), and you know the lengths of all four sides, you can utilize Heron's formula to find the area. Then, using the area and base lengths (as in Method 1), you can calculate the height. Heron's formula finds the area of a triangle given its three side lengths. To apply this to an isosceles trapezium, you divide the trapezium into two triangles and a rectangle. Finding the area of the two triangles using Heron's formula and summing it with the area of the rectangle allows for finding the total area, and then ultimately the height.
Considerations for this method:
- This method is restricted to isosceles trapezia.
- Applying Heron's formula can be time-consuming, and the calculations involved may be complex.
Real-World Applications of Finding the Height of a Trapezium
The ability to calculate the height of a trapezium has numerous practical applications across various fields:
-
Architecture and Construction: Determining the area of irregularly shaped plots of land, calculating the volume of structures with trapezoidal cross-sections, and designing roof structures.
-
Surveying and Land Measurement: Calculating the area of land parcels with trapezoidal shapes, crucial for property valuation and land management.
-
Engineering: Designing components with trapezoidal shapes, such as retaining walls, channels, and structural supports. Calculating the area is vital for load-bearing capacity and stability assessments.
-
Graphic Design and Computer-Aided Design (CAD): Creating and manipulating trapezoidal shapes in design software. Accurate height calculations are essential for precise dimensions and scaling.
Conclusion
Finding the height of a trapezium involves a variety of methods, each suited to different circumstances and levels of available information. From the straightforward application of the area formula to the more complex utilization of coordinate geometry and trigonometry, the choice of method depends on the specific problem at hand. A solid understanding of these techniques equips you to tackle real-world problems across various disciplines and promotes a deeper appreciation for geometrical principles. Remember to choose the method that best suits the given information and your level of mathematical expertise, paying careful attention to detail to minimize calculation errors. Practice is key to mastering these methods and confidently tackling any trapezium height problem that comes your way.
Latest Posts
Latest Posts
-
The Basic Structural Unit Of Compact Bone Is The
Apr 08, 2025
-
What Is The Quotient Of 18 1000
Apr 08, 2025
-
A Cat Walks In A Straight Line
Apr 08, 2025
-
How To Write A Conjecture In Math
Apr 08, 2025
-
Which Of The Following Is A Good Conductor Of Heat
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Find The Height Of A Trapezium . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.