Find The Area Of The Figure Shown
News Leon
Apr 03, 2025 · 6 min read
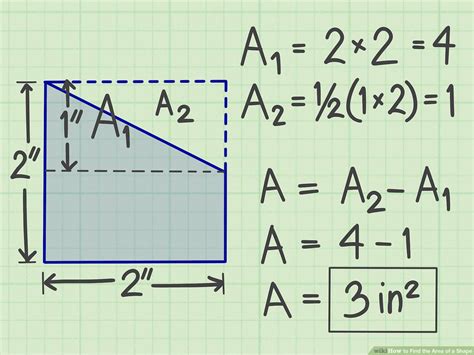
Table of Contents
Find the Area of the Figure Shown: A Comprehensive Guide
Finding the area of a geometric figure is a fundamental concept in mathematics with widespread applications in various fields, from architecture and engineering to computer graphics and data analysis. While simple shapes like squares and rectangles have straightforward area calculations, more complex figures often require a strategic approach combining different techniques. This comprehensive guide will walk you through various methods to determine the area of irregular shapes, focusing on practical strategies and problem-solving techniques. We will explore a range of shapes and scenarios, providing clear explanations and illustrative examples.
Understanding Area: The Basics
Before delving into complex figures, let's solidify our understanding of the fundamental concept of area. Area refers to the amount of two-dimensional space a shape occupies. It's measured in square units, such as square centimeters (cm²), square meters (m²), or square feet (ft²).
The area formulas for basic shapes are:
- Rectangle: Area = length × width
- Square: Area = side × side (or side²)
- Triangle: Area = (1/2) × base × height
- Circle: Area = π × radius² (where π ≈ 3.14159)
These formulas serve as building blocks for calculating the area of more intricate shapes.
Decomposing Complex Figures: The Divide and Conquer Strategy
Many irregularly shaped figures can be broken down into simpler shapes whose areas are easily calculated. This "divide and conquer" approach is a highly effective method.
Steps:
- Identify the constituent shapes: Carefully examine the figure and identify the basic shapes (rectangles, triangles, circles, etc.) that make up the whole.
- Calculate the area of each shape: Use the appropriate formula to find the area of each individual shape. Remember to accurately measure or extract necessary dimensions (length, width, base, height, radius).
- Sum the individual areas: Add the areas of all the constituent shapes to find the total area of the complex figure.
Example:
Imagine a figure resembling an L-shape. It can be divided into two rectangles. Let's say one rectangle has a length of 8 units and a width of 4 units, while the other has a length of 6 units and a width of 3 units.
- Area of Rectangle 1: 8 units × 4 units = 32 square units
- Area of Rectangle 2: 6 units × 3 units = 18 square units
- Total Area: 32 square units + 18 square units = 50 square units
Using Subtraction to Find Area: The "Outer-Inner" Method
Sometimes, it's easier to calculate the area of a larger, simpler shape encompassing the target figure and then subtract the area of the extra parts. This "outer-inner" method is particularly useful when a shape has a hole or a cutout.
Steps:
- Enclose the figure: Draw a larger, simpler shape (usually a rectangle or square) that completely encloses the target figure.
- Calculate the area of the enclosing shape: Use the appropriate formula to find the area of this larger shape.
- Calculate the area of the subtracted parts: Determine the area of the portions of the enclosing shape that are outside the target figure.
- Subtract the areas: Subtract the area of the subtracted parts from the area of the enclosing shape to obtain the area of the target figure.
Example:
Consider a square with a circular hole in the center.
- Enclosing Shape: The area of the square (let's say side length is 10 units) is 100 square units.
- Subtracted Part: The area of the circle (let's say radius is 2 units) is π × 2² ≈ 12.57 square units.
- Area of the Figure: 100 square units - 12.57 square units ≈ 87.43 square units
Dealing with Irregular Polygons: Approximation Techniques
Irregular polygons, which lack the regularity of shapes like squares or rectangles, can be challenging. Approximation techniques are often necessary:
- Triangulation: Divide the polygon into multiple triangles. Calculate the area of each triangle using the formula (1/2) × base × height, and sum the individual areas. This method works well for polygons with straight sides. The accuracy depends on the number of triangles used; more triangles generally lead to a more accurate approximation.
- Grid Method: Overlay a grid over the figure. Count the number of complete squares within the figure and estimate the area of partial squares. This method is less precise but can be useful for quickly estimating the area of highly irregular figures.
- Coordinate Geometry: If the vertices of the polygon are known in a coordinate system (x, y coordinates), the area can be calculated using a determinant formula or by breaking the polygon into trapezoids.
Advanced Techniques: Integration and Calculus
For extremely complex shapes that are not easily decomposable, integral calculus provides a powerful tool for precise area calculation. The area under a curve is calculated using definite integrals. This technique is beyond the scope of this introductory guide but is crucial for advanced applications.
Practical Applications and Real-World Examples
The ability to calculate the area of various shapes is crucial in numerous fields:
- Architecture and Engineering: Calculating the area of rooms, land plots, or building materials is essential for planning, construction, and cost estimation.
- Agriculture: Determining the size of fields for planting, irrigation, or fertilizer application relies heavily on area calculations.
- Computer Graphics: Area calculations are fundamental in rendering images, creating 3D models, and performing spatial analyses.
- Cartography: Measuring the area of countries, regions, or other geographic features requires sophisticated area calculation techniques.
- Data Analysis: Area-based methods are used in various statistical and data visualization techniques.
Tips and Tricks for Accurate Area Calculation
- Precise Measurements: Accurate measurements are crucial. Use appropriate tools (rulers, measuring tapes, etc.) to obtain precise dimensions.
- Check Your Work: Always double-check your calculations to avoid errors.
- Use Diagrams: Sketching diagrams of the figures helps visualize the constituent shapes and plan your approach.
- Break Down Complex Shapes: Don't be afraid to divide complex shapes into smaller, simpler shapes.
- Understand Limitations: Approximation methods are not always perfectly accurate. Be aware of the potential for error when using these techniques.
Conclusion
Calculating the area of a figure, whether simple or complex, is a multifaceted process requiring a strategic approach. This guide has explored various methods – from decomposing shapes into basic units to using advanced mathematical techniques – illustrating their application through practical examples. Mastering these techniques will not only enhance your mathematical skills but also provide you with valuable tools for tackling real-world problems across diverse disciplines. Remember to practice regularly and utilize the most appropriate method for the figure at hand to ensure accuracy and efficiency. By combining a sound understanding of geometry with a strategic approach, you can confidently tackle any area calculation challenge that comes your way.
Latest Posts
Latest Posts
-
How Does An Amoeba Obtain Food
Apr 04, 2025
-
Bureaucracy Is Based On Which Of The Following Principles
Apr 04, 2025
-
Why Hydrogen Is In Group 1
Apr 04, 2025
-
What Is The Prime Factorization Of 120
Apr 04, 2025
-
Do Nonmetals Gain Or Lose Electrons
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of The Figure Shown . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
