Find Ac If Ab 16 And Bc 12
News Leon
May 04, 2025 · 4 min read
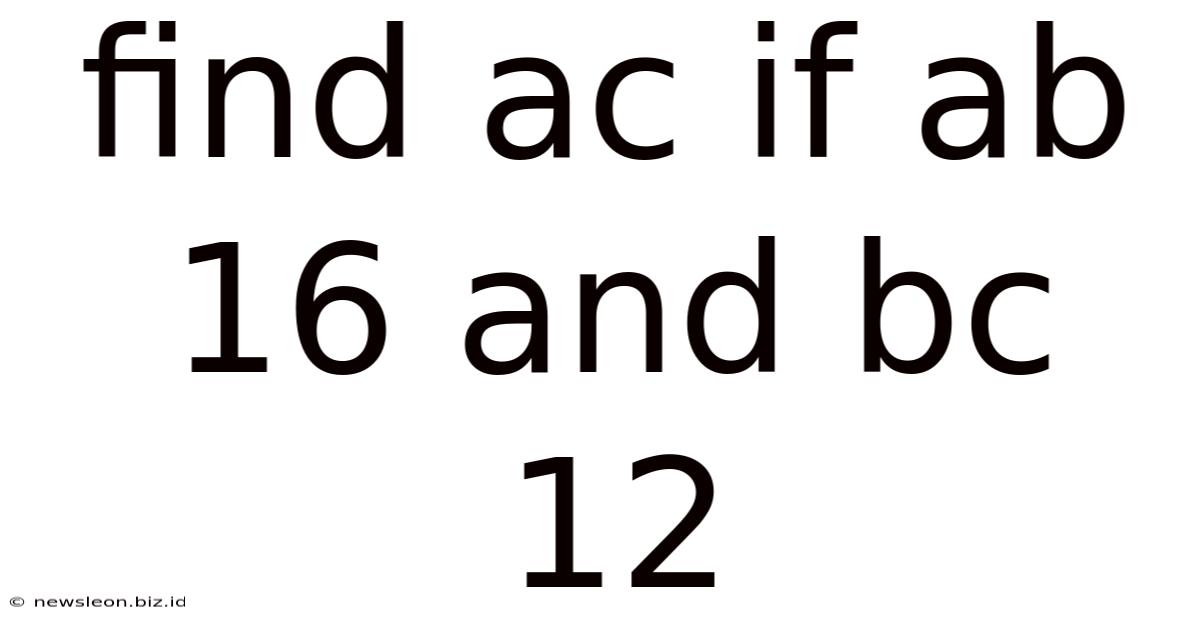
Table of Contents
Find AC if AB = 16 and BC = 12: Exploring Geometric Solutions
This article delves into the problem of determining the length of side AC in a triangle, given the lengths of sides AB and BC. While seemingly straightforward, this problem highlights the importance of understanding different geometric principles and the need for additional information to arrive at a definitive solution. We'll explore various scenarios and mathematical approaches to solve this, emphasizing the crucial role of context in geometric problems.
The Ambiguity of the Problem
The core challenge lies in the inherent ambiguity of the problem statement. Knowing only the lengths of AB (16) and BC (12) is insufficient to uniquely determine the length of AC. To illustrate this, consider the following scenarios:
Scenario 1: Triangle ABC is a right-angled triangle
If we assume that angle B is a right angle (90°), then we can apply the Pythagorean theorem. The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
-
Hypotenuse AB: If AB (16) is the hypotenuse, then:
- AC² + BC² = AB²
- AC² + 12² = 16²
- AC² + 144 = 256
- AC² = 112
- AC = √112 ≈ 10.58
-
Hypotenuse AC: If AC is the hypotenuse, then:
- AB² + BC² = AC²
- 16² + 12² = AC²
- 256 + 144 = AC²
- AC² = 400
- AC = 20
This demonstrates that even with the additional assumption of a right-angled triangle, we obtain two different possible lengths for AC depending on which side is the hypotenuse.
Scenario 2: Triangle ABC is an obtuse-angled triangle
If triangle ABC is obtuse-angled (meaning one angle is greater than 90°), then the Pythagorean theorem does not directly apply. The length of AC would depend on the size of angle B. There’s a range of possible values for AC depending on the measure of angle B. The Law of Cosines provides a more general approach in this scenario:
- Law of Cosines: AC² = AB² + BC² - 2(AB)(BC)cos(B)
To find AC, we would need the value of angle B. Without knowing angle B, we cannot determine the length of AC. The Law of Cosines allows us to calculate AC if we know the lengths of two sides and the included angle.
Scenario 3: Triangle ABC is an acute-angled triangle
Similarly, if triangle ABC is acute-angled (all angles less than 90°), the Pythagorean theorem doesn't directly apply. Again, we would need additional information, such as the measure of one of the angles (besides angle B), to use the Law of Sines or the Law of Cosines to find AC.
- Law of Sines: a/sin(A) = b/sin(B) = c/sin(C)
This law relates the ratio of the length of a side to the sine of its opposite angle. Knowing two angles and one side, or two sides and one angle (other than the included angle), allows us to solve for the remaining sides and angles.
The Importance of Additional Information
The examples above clearly illustrate that the problem of finding AC with only AB and BC given is underdetermined. We need at least one additional piece of information to solve it definitively. This could be:
- The measure of angle B: This allows direct application of the Law of Cosines.
- The measure of angle A or C: This combined with the Law of Sines or Cosines would allow us to solve the triangle.
- The area of the triangle: Knowing the area provides an additional constraint that can be used in conjunction with other formulas to find AC.
- The nature of the triangle: Specifying whether the triangle is isosceles, equilateral, or right-angled provides crucial information.
Illustrative Examples with Additional Information
Let's illustrate with examples where we add the necessary information:
Example 1: Angle B = 60°
Using the Law of Cosines:
AC² = 16² + 12² - 2(16)(12)cos(60°) AC² = 256 + 144 - 384(0.5) AC² = 400 - 192 AC² = 208 AC = √208 ≈ 14.42
Example 2: Triangle ABC is an isosceles triangle with AB = AC
In this case, AC = AB = 16.
Example 3: The area of triangle ABC is 96 square units
The area of a triangle can be calculated using the formula: Area = (1/2)ab sin(C). Here, we have:
96 = (1/2)(16)(12) sin(C) 96 = 96 sin(C) sin(C) = 1 C = 90°
Therefore, the triangle is a right-angled triangle with the right angle at C, allowing us to use the Pythagorean theorem as shown in Scenario 1 (Hypotenuse AC). We find AC = 20.
Conclusion: Context is Key in Geometry
Determining the length of AC, given only AB and BC, highlights the critical importance of context in geometry. The problem is inherently ambiguous without additional information specifying the type of triangle or at least one angle or the area. Understanding various geometric principles, such as the Pythagorean theorem, the Law of Cosines, and the Law of Sines, provides the tools needed to solve such problems once sufficient constraints are available. Always carefully analyze the given information and identify any missing pieces required to reach a unique and accurate solution. Remember to consider different scenarios and apply the appropriate geometric theorems to find the solution. The ability to adapt your approach based on the available information is a crucial skill in geometry and mathematics in general.
Latest Posts
Related Post
Thank you for visiting our website which covers about Find Ac If Ab 16 And Bc 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.