Factor X 4 5x 2 4
News Leon
Apr 05, 2025 · 5 min read
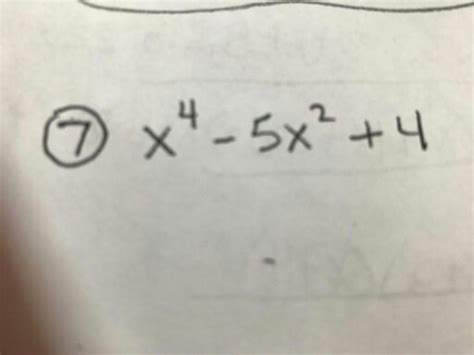
Table of Contents
Factoring the Quadratic Expression: x² + 5x + 4
This article delves into the process of factoring the quadratic expression x² + 5x + 4. We will explore various methods, explain the underlying concepts, and provide examples to solidify your understanding. Mastering quadratic factoring is crucial for various mathematical applications, from solving equations to graphing parabolas. Let's get started!
Understanding Quadratic Expressions
Before diving into the factoring process, let's clarify what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form is ax² + bx + c, where a, b, and c are constants, and a ≠ 0. In our specific expression, x² + 5x + 4, we have a = 1, b = 5, and c = 4.
Method 1: Factoring by Inspection (Trial and Error)
This method involves finding two numbers that add up to the coefficient of the x term (b = 5) and multiply to the constant term (c = 4). Let's break it down:
-
Identify the factors of the constant term (c = 4): The pairs of factors of 4 are (1, 4) and (2, 2).
-
Check which pair adds up to the coefficient of the x term (b = 5): The pair (1, 4) adds up to 5.
-
Construct the factored form: Since the pair (1, 4) satisfies both conditions, we can write the factored form as (x + 1)(x + 4).
-
Verification: To verify, we can expand the factored form using the FOIL (First, Outer, Inner, Last) method:
(x + 1)(x + 4) = x² + 4x + x + 4 = x² + 5x + 4
This confirms that our factoring is correct.
Method 2: The AC Method (For expressions where a ≠ 1)
While our example has a = 1, the AC method is valuable for factoring quadratic expressions where the coefficient of x² is not 1. Let's illustrate this method with a different example, then apply the understanding back to our original problem.
Consider the quadratic expression 2x² + 7x + 3.
-
Multiply 'a' and 'c': In this case, a * c = 2 * 3 = 6.
-
Find two numbers that add up to 'b' and multiply to 'ac': We need two numbers that add up to 7 (our 'b' value) and multiply to 6. These numbers are 1 and 6.
-
Rewrite the expression: Rewrite the middle term (7x) using these two numbers: 2x² + 6x + x + 3
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
2x(x + 3) + 1(x + 3)
-
Factor out the common binomial: Notice that both terms have (x + 3) as a common factor:
(x + 3)(2x + 1)
Therefore, the factored form of 2x² + 7x + 3 is (x + 3)(2x + 1).
Applying the understanding to our original problem (x² + 5x + 4): Even though the AC method is designed for a ≠ 1, we can conceptually apply it. ac = 14 = 4. The factors of 4 that add up to 5 are 1 and 4. This leads us to the same result as the inspection method: (x+1)(x+4).
Method 3: Using the Quadratic Formula
The quadratic formula provides a general solution for finding the roots (or zeros) of any quadratic equation of the form ax² + bx + c = 0. While not a direct factoring method, it helps determine the factors.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression x² + 5x + 4 = 0, we have a = 1, b = 5, and c = 4. Plugging these values into the formula:
x = [-5 ± √(5² - 4 * 1 * 4)] / 2 * 1 = [-5 ± √9] / 2 = [-5 ± 3] / 2
This gives us two solutions:
x₁ = (-5 + 3) / 2 = -1 x₂ = (-5 - 3) / 2 = -4
These solutions correspond to the factors (x + 1) and (x + 4), as a root of -1 implies a factor of (x + 1) and a root of -4 implies a factor of (x + 4).
Applications of Factoring Quadratic Expressions
The ability to factor quadratic expressions is fundamental in various mathematical contexts:
-
Solving Quadratic Equations: Factoring allows us to easily solve quadratic equations by setting each factor equal to zero and solving for x. For example, to solve x² + 5x + 4 = 0, we set (x + 1)(x + 4) = 0, which gives us x = -1 and x = -4.
-
Graphing Parabolas: The factored form of a quadratic expression reveals the x-intercepts (where the parabola crosses the x-axis) of its corresponding graph. The x-intercepts of y = x² + 5x + 4 are -1 and -4.
-
Simplifying Algebraic Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and solve.
-
Calculus: Factoring plays a critical role in calculus, particularly in finding derivatives and integrals.
-
Physics and Engineering: Quadratic equations and their solutions are prevalent in modeling various physical phenomena, such as projectile motion, and in engineering design.
Advanced Factoring Techniques (Beyond the Scope of x² + 5x + 4)
While the methods discussed above are sufficient for factoring our specific example, more advanced techniques exist for factoring more complex quadratic expressions or those with non-integer coefficients. These include:
-
Completing the Square: This technique involves manipulating the quadratic expression to create a perfect square trinomial, which can then be factored easily.
-
Difference of Squares: This method applies to expressions of the form a² - b², which factors to (a + b)(a - b).
-
Sum and Difference of Cubes: Similar to the difference of squares, this method factors expressions of the form a³ + b³ and a³ - b³.
-
Grouping: This technique is useful for factoring expressions with four or more terms.
Conclusion
Factoring the quadratic expression x² + 5x + 4 is a straightforward process once you understand the underlying principles. Whether you use the inspection method, the AC method, or derive the factors from the quadratic formula, the result remains the same: (x + 1)(x + 4). Mastering this fundamental skill is crucial for success in algebra and its numerous applications in various fields. Remember to practice regularly to strengthen your understanding and build confidence in tackling more complex quadratic expressions. By understanding the different methods and their applications, you'll be well-equipped to handle various quadratic factoring problems effectively. The key is practice and understanding the underlying mathematical concepts. Don't be afraid to experiment with different techniques to find the one that best suits your problem-solving style.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factor X 4 5x 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
