Factor X 2 2xy Y 2
News Leon
May 03, 2025 · 5 min read
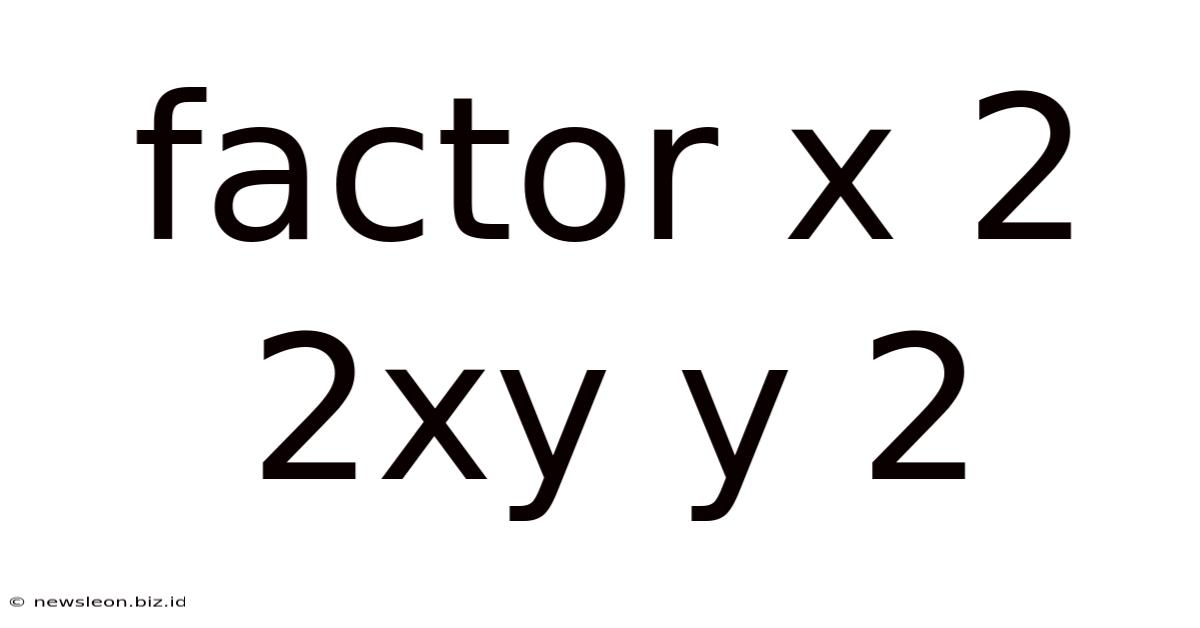
Table of Contents
Understanding and Applying the Factorization of x² + 2xy + y²
The expression x² + 2xy + y² is a fundamental concept in algebra, representing a perfect square trinomial. Understanding its factorization is crucial for various mathematical applications, from simplifying complex expressions to solving quadratic equations and even venturing into higher-level mathematical concepts. This article will provide a comprehensive exploration of this expression, covering its factorization, applications, and related concepts.
What is a Perfect Square Trinomial?
Before delving into the factorization of x² + 2xy + y², let's define what a perfect square trinomial is. A perfect square trinomial is a trinomial (a polynomial with three terms) that can be factored into the square of a binomial. In simpler terms, it's a trinomial that results from squaring a binomial expression. The general form of a perfect square trinomial is:
a² + 2ab + b² = (a + b)²
or
a² - 2ab + b² = (a - b)²
Notice the pattern: the first and last terms are perfect squares (a² and b²), and the middle term is twice the product of the square roots of the first and last terms (2ab). This pattern is essential for recognizing and factoring perfect square trinomials efficiently.
Factoring x² + 2xy + y²
Our expression, x² + 2xy + y², perfectly fits the form of a perfect square trinomial. Let's break down why and how it factors:
-
Identify the perfect squares: Observe that x² is the square of x (x²) and y² is the square of y (y²).
-
Check the middle term: The middle term, 2xy, is twice the product of x and y (2 * x * y). This confirms it aligns with the pattern of a perfect square trinomial.
-
Apply the formula: Using the formula a² + 2ab + b² = (a + b)², we can directly factor x² + 2xy + y²:
x² + 2xy + y² = (x + y)²
This factorization means that x² + 2xy + y² is equivalent to the square of the binomial (x + y). This seemingly simple factorization has significant implications in various mathematical contexts.
Applications of the Factorization
The factorization of x² + 2xy + y² = (x + y)² has widespread applications in many areas of mathematics, including:
1. Simplifying Algebraic Expressions
When encountered within more complex algebraic expressions, this factorization can simplify them considerably. For example:
(x² + 2xy + y²) + 3x - 2y can be simplified to (x + y)² + 3x - 2y
This makes further manipulation and solving much easier.
2. Solving Quadratic Equations
Perfect square trinomials often appear in quadratic equations. Understanding their factorization can significantly speed up the solving process. For instance, consider the quadratic equation:
x² + 2xy + y² - 4 = 0
Using the factorization, this equation can be rewritten as:
(x + y)² - 4 = 0
This is now much simpler to solve, using basic algebraic manipulation.
3. Geometry and Area Calculations
This factorization has a direct geometric interpretation. Consider a square with sides of length (x + y). The area of this square can be calculated as (x + y)². Expanding this expression gives us x² + 2xy + y². This shows that the area of the square can be broken down into three parts: a square with area x², a square with area y², and two rectangles each with area xy.
4. Calculus and Derivatives
In calculus, understanding the factorization of perfect square trinomials can be beneficial in simplifying expressions before differentiation or integration. The ability to recognize and factor these forms can simplify complex derivative calculations.
5. Advanced Mathematical Concepts
The concept extends to more advanced mathematical fields like linear algebra and multivariable calculus where the same principles apply but in higher dimensions. Understanding the fundamental factorization builds a solid base for comprehending more intricate mathematical structures.
Related Concepts and Extensions
Several related concepts build upon the understanding of factoring x² + 2xy + y²:
-
Difference of Squares: While we focused on the sum of squares in a trinomial, understanding the difference of squares (a² - b² = (a + b)(a - b)) is equally important. Both are frequently used in algebraic manipulation.
-
Completing the Square: This technique involves manipulating quadratic expressions to create a perfect square trinomial, allowing for easier solution of quadratic equations. Understanding perfect square trinomials is fundamental to completing the square method.
-
Polynomial Factorization: The factorization of x² + 2xy + y² is a specific case within the broader concept of polynomial factorization. Mastering this fundamental case improves abilities to factor more complex polynomials.
-
Binomial Theorem: The binomial theorem describes the expansion of (a + b)ⁿ for any positive integer n. The case of n = 2 directly relates to the factorization of x² + 2xy + y².
Practical Exercises and Examples
Let's solidify our understanding with some examples and exercises:
Example 1: Factor 4x² + 12xy + 9y²
This is a perfect square trinomial. Notice (2x)² = 4x², (3y)² = 9y², and 2 * (2x) * (3y) = 12xy. Therefore, the factorization is:
(2x + 3y)²
Example 2: Solve the equation x² + 6x + 9 = 16
This equation can be rewritten as a perfect square trinomial:
(x + 3)² = 16
Taking the square root of both sides, we get:
x + 3 = ±4
Solving for x gives us two solutions: x = 1 and x = -7
Exercise 1: Factor 9a² - 24ab + 16b²
Exercise 2: Solve the equation 25m² + 20m + 4 = 0
Exercise 3: Simplify (x² + 4xy + 4y²) / (x + 2y)
Conclusion
The factorization of x² + 2xy + y² = (x + y)² is a cornerstone of algebra. Understanding this factorization is not just about memorizing a formula; it's about grasping the underlying mathematical structure and its practical applications. From simplifying expressions and solving equations to gaining a deeper appreciation for geometric interpretations and more advanced mathematical concepts, this seemingly simple factorization provides a robust foundation for further mathematical exploration. By mastering this fundamental concept, you significantly enhance your problem-solving abilities in numerous mathematical fields. The provided exercises and examples will help solidify this understanding and prepare you to confidently apply this knowledge in more challenging contexts. Remember to practice regularly to improve your fluency and accuracy in factoring perfect square trinomials.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factor X 2 2xy Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.