Equation Of Line Parallel To Y Axis
News Leon
Apr 06, 2025 · 6 min read
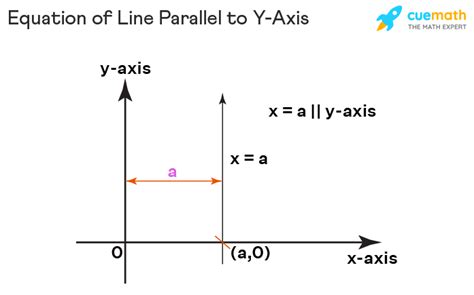
Table of Contents
The Equation of a Line Parallel to the Y-Axis: A Comprehensive Guide
The equation of a line parallel to the y-axis represents a unique and fundamental concept in coordinate geometry. Unlike lines with slopes, lines parallel to the y-axis possess an infinite slope, leading to a distinct equation and interesting geometric properties. This comprehensive guide will explore the equation, its derivation, its applications, and related concepts in detail.
Understanding the Y-Axis and Parallel Lines
Before diving into the equation, let's establish a firm understanding of the y-axis and the concept of parallel lines.
The y-axis is the vertical line in a Cartesian coordinate system that runs through the origin (0,0). It represents all points with an x-coordinate of 0. Any point on the y-axis can be represented as (0, y), where 'y' can be any real number.
Parallel lines are lines that lie in the same plane and never intersect, regardless of how far they are extended. They maintain a constant distance from each other. Crucially, parallel lines have the same slope (with the exception of vertical lines, as we will see).
Deriving the Equation: Why it's x = k
The standard equation of a line is often expressed as y = mx + c, where 'm' represents the slope and 'c' represents the y-intercept (the point where the line crosses the y-axis). However, this equation doesn't apply to lines parallel to the y-axis.
Why? Because lines parallel to the y-axis have an undefined slope. The slope is calculated as the change in y divided by the change in x (Δy/Δx). For a vertical line, the change in x (Δx) is always zero. Division by zero is undefined in mathematics. Therefore, the standard slope-intercept form breaks down.
Instead, the equation of a line parallel to the y-axis is expressed as:
x = k
where 'k' is a constant representing the x-coordinate of every point on the line. This means that no matter what the y-coordinate is, the x-coordinate remains constant at 'k'.
Visualizing x = k
Imagine a vertical line passing through the point (3, 0). Every point on this line will have an x-coordinate of 3, regardless of its y-coordinate. This line can be represented by the equation x = 3. Similarly, a line passing through (-2, 0) would have the equation x = -2. The constant 'k' defines the line's position along the x-axis.
Properties and Characteristics of x = k
The equation x = k has several key properties:
- Undefined slope: As previously discussed, the slope is undefined.
- Constant x-coordinate: The x-coordinate is always equal to 'k'. This is the defining characteristic.
- Infinite number of y-coordinates: The line extends infinitely in both the positive and negative y-directions, meaning there are an infinite number of possible y-coordinates for any given x-coordinate ('k').
- Parallel to the y-axis: By definition, it's parallel to the y-axis.
- Perpendicular to the x-axis: All lines of the form x = k are perpendicular to the x-axis.
- Simple equation: The equation is remarkably simple and straightforward.
Applications and Real-World Examples
While seemingly simple, the equation x = k has practical applications across various fields:
- Computer Graphics: In computer graphics and game development, defining vertical lines using x = k is crucial for creating boundaries, walls, and other vertical structures.
- Engineering and Construction: In engineering and construction, the equation is used to represent vertical supports, columns, and boundaries in blueprints and models.
- Physics: In physics, it can represent the path of an object moving strictly vertically (ignoring other forces).
- Mathematics: It's a fundamental concept in coordinate geometry, essential for understanding lines and their properties.
Distinguishing x = k from Other Line Equations
It's important to distinguish x = k from other common line equations:
- y = mx + c (slope-intercept form): This represents a line with a defined slope and y-intercept. It does not represent vertical lines.
- Ax + By = C (standard form): In this form, a vertical line would be represented by an equation where B = 0 and A ≠ 0. This would simplify to Ax = C, or x = C/A, which is equivalent to x = k.
- y - y₁ = m(x - x₁): This is the point-slope form. It cannot represent vertical lines because the slope, 'm', is undefined.
Solving Problems Involving x = k
Let's look at a few example problems to solidify our understanding:
Problem 1: Find the equation of the line parallel to the y-axis that passes through the point (5, 2).
Solution: Since the line is parallel to the y-axis, its equation will be of the form x = k. The x-coordinate of the given point is 5, therefore the equation of the line is x = 5.
Problem 2: Determine if the points (2, 1) and (2, 5) lie on the same line. If so, what is the equation of the line?
Solution: Both points have the same x-coordinate, x = 2. Therefore, they lie on the same vertical line. The equation of the line is x = 2.
Problem 3: Find the intersection point of the lines x = 4 and y = 2x - 1.
Solution: The line x = 4 represents all points with an x-coordinate of 4. To find the intersection point, substitute x = 4 into the equation y = 2x - 1: y = 2(4) - 1 = 7. The intersection point is (4, 7).
Advanced Concepts and Extensions
While the basic concept of x = k is relatively straightforward, it can be extended to more complex scenarios:
- Systems of Equations: Solving systems of equations involving x = k and other linear equations often leads to straightforward solutions.
- Distance from a Point to a Line: The distance between a point and a vertical line x = k is simply the absolute difference between the point's x-coordinate and k.
- Regions Defined by Inequalities: Inequalities involving x = k, such as x > k or x < k, define regions in the Cartesian plane.
Conclusion
The seemingly simple equation x = k represents a powerful and fundamental concept in coordinate geometry. Its simplicity belies its importance in various mathematical and real-world applications. Understanding its derivation, properties, and applications is crucial for anyone working with coordinate systems and linear equations. Mastering this concept forms a solid foundation for more advanced studies in mathematics, computer science, and engineering. Through careful consideration of its unique characteristics and practical applications, we can appreciate its significance within the broader context of analytical geometry. The equation x = k is not merely a simple formula; it's a key element in unlocking a deeper understanding of lines and spatial relationships.
Latest Posts
Latest Posts
-
Which Of The Following Is Not True Regarding Viruses
Apr 09, 2025
-
What Is One Difference Between A Mixture And A Compound
Apr 09, 2025
-
Which Of The Following Is Not A Membrane Bound Organelle
Apr 09, 2025
-
Determine The Number Of 4 D Electrons In Mo
Apr 09, 2025
-
Select The Correct Statement About Plant Growth
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Equation Of Line Parallel To Y Axis . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.