Electric Field Of A Sphere Formula
News Leon
Apr 03, 2025 · 6 min read
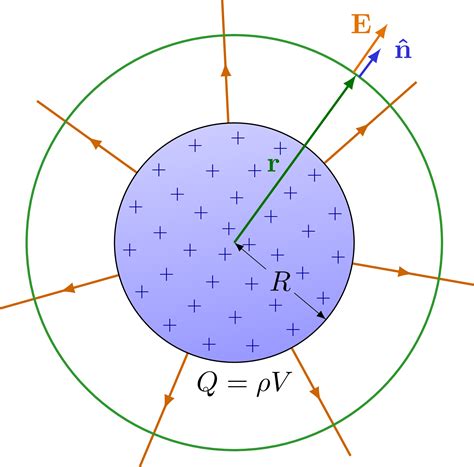
Table of Contents
- Electric Field Of A Sphere Formula
- Table of Contents
- Electric Field of a Sphere: A Comprehensive Guide
- Understanding the Fundamentals: Coulomb's Law and Electric Fields
- Electric Field of a Uniformly Charged Sphere
- Case 1: Outside the Sphere (r > R)
- Case 2: Inside the Sphere (r < R)
- Electric Field of a Non-Uniformly Charged Sphere
- Conducting and Insulating Spheres
- Conducting Sphere
- Insulating Sphere
- Applications of Electric Field of a Sphere
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Electric Field of a Sphere: A Comprehensive Guide
The electric field of a sphere, a fundamental concept in electrostatics, plays a crucial role in understanding various physical phenomena. This comprehensive guide delves into the intricacies of calculating the electric field for different scenarios, exploring both theoretical derivations and practical applications. We'll cover uniformly charged spheres, spheres with non-uniform charge distributions, and the influence of conductors and insulators.
Understanding the Fundamentals: Coulomb's Law and Electric Fields
Before diving into the specifics of spherical charge distributions, let's refresh our understanding of fundamental concepts. Coulomb's Law provides the foundation for calculating the electric force between two point charges:
F = k * |q1 * q2| / r^2
where:
Fis the force between the chargeskis Coulomb's constant (approximately 8.98755 × 10⁹ N⋅m²/C²)q1andq2are the magnitudes of the chargesris the distance between the charges
The electric field (E) at a point in space is defined as the force per unit charge experienced by a small positive test charge placed at that point:
E = F / q
Therefore, the electric field due to a point charge q at a distance r is given by:
E = k * q / r^2
This fundamental relationship forms the basis for calculating the electric field of more complex charge distributions, including spheres.
Electric Field of a Uniformly Charged Sphere
Let's consider a sphere of radius R carrying a total charge Q uniformly distributed throughout its volume. To calculate the electric field at a distance r from the center of the sphere, we'll consider two cases:
Case 1: Outside the Sphere (r > R)
When the point of interest lies outside the sphere (r > R), the sphere can be treated as a point charge located at its center. This is a consequence of Gauss's Law, which states that the flux of the electric field through any closed surface is proportional to the enclosed charge. Using Gauss's Law and considering a spherical Gaussian surface with radius r encompassing the charged sphere, we obtain:
E * 4πr² = Q / ε₀
where:
ε₀is the permittivity of free space (approximately 8.854 × 10⁻¹² C²/N⋅m²)
Solving for the electric field E, we get:
E = (k * Q) / r²
This equation is identical to the electric field of a point charge, confirming our earlier assertion. The electric field outside a uniformly charged sphere behaves as if all the charge were concentrated at its center.
Case 2: Inside the Sphere (r < R)
The situation inside the sphere is significantly different. Again, using Gauss's Law, we construct a spherical Gaussian surface with radius r (r < R). The charge enclosed within this Gaussian surface is proportional to the volume enclosed:
Q_enclosed = Q * (r³/R³)
Applying Gauss's Law:
E * 4πr² = (Q * r³) / (R³ * ε₀)
Solving for the electric field E:
E = (k * Q * r) / R³
This equation reveals a crucial difference: the electric field inside a uniformly charged sphere is directly proportional to the distance r from the center. At the center of the sphere (r = 0), the electric field is zero.
Electric Field of a Non-Uniformly Charged Sphere
Calculating the electric field for a sphere with a non-uniform charge distribution becomes significantly more complex. The method of solving this depends entirely on the specific nature of the charge distribution. There isn't a single, universal formula. However, we can outline a general approach:
-
Define the Charge Density: First, we must define the charge density, ρ(r, θ, φ), which describes how the charge is distributed throughout the sphere's volume. This could be a function of the radial distance (r), the polar angle (θ), and/or the azimuthal angle (φ) in spherical coordinates.
-
Apply Coulomb's Law (or Gauss's Law): For a non-uniform distribution, applying Coulomb's Law directly usually involves intricate integration over the volume of the sphere. Gauss's Law can sometimes simplify the process if a suitable Gaussian surface can be chosen. However, symmetry is crucial for Gauss's Law to be effective.
-
Integrate to Find the Electric Field: The electric field at a given point is determined by integrating the contributions from each infinitesimal charge element within the sphere. This often leads to complex multiple integrals that may require numerical techniques for evaluation.
-
Consider Symmetry: Utilizing any inherent symmetry in the charge distribution will simplify the calculations drastically. For instance, spherical symmetry, cylindrical symmetry, or even planar symmetry can make the problem more tractable.
Conducting and Insulating Spheres
The nature of the sphere (conducting or insulating) significantly impacts its electric field.
Conducting Sphere
A conducting sphere, in electrostatic equilibrium, has the following crucial properties:
- Charge resides on the surface: All excess charge on a conductor resides on its surface.
- Electric field inside is zero: The electric field inside a conducting sphere is zero. Any internal electric field would cause charges to move until equilibrium is reached.
- Electric field outside is identical to a point charge: The electric field outside a conducting sphere is identical to that of a point charge located at its center, with the total charge Q equal to the total charge on the sphere.
Therefore, the electric field outside a conducting sphere is given by:
E = (k * Q) / r² (r > R)
and the electric field inside is:
E = 0 (r < R)
Insulating Sphere
For an insulating sphere, the charge can be distributed throughout its volume. The electric field calculations depend on the specific charge distribution, as discussed in the section on non-uniformly charged spheres. However, if the charge is uniformly distributed, the formulas derived earlier apply.
Applications of Electric Field of a Sphere
The electric field of a sphere has numerous applications across diverse fields:
- Atomic Physics: The understanding of the electric field surrounding an atomic nucleus is crucial for understanding atomic structure and electron behavior.
- Electrostatic Precipitation: This technology utilizes the electric field of charged spheres to remove particulate matter from industrial emissions.
- Medical Imaging: Certain medical imaging techniques rely on the principles of electric fields and charged particles.
- Capacitors: Spherical capacitors utilize the electric field between concentric charged spheres for energy storage.
- Weather phenomena: Understanding the electric fields associated with charged raindrops and ice crystals is crucial for comprehending lightning and other weather events.
Conclusion
The electric field of a sphere, seemingly a simple concept, encompasses a rich tapestry of mathematical and physical intricacies. From the straightforward case of a uniformly charged sphere to the complexities of non-uniform distributions and the behavior of conductors and insulators, a thorough understanding is essential for grasping numerous phenomena in physics and engineering. This guide has provided a solid foundation for tackling problems related to the electric field of spheres, emphasizing both theoretical derivations and practical applications. Remember that careful consideration of the charge distribution and the properties of the material (conductor or insulator) is crucial for accurate calculations.
Latest Posts
Latest Posts
-
Which Best Describes The Law Of Independent Assortment
Apr 06, 2025
-
You Should Always Assign The Needs Met Rating Before
Apr 06, 2025
-
Which Is The Most Densely Populated Continent
Apr 06, 2025
-
Average Velocity On Velocity Time Graph
Apr 06, 2025
-
The First Scientist To Observe Cells With A Microscope Was
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Of A Sphere Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
