Electric Field For Infinite Line Of Charge
News Leon
Apr 02, 2025 · 7 min read
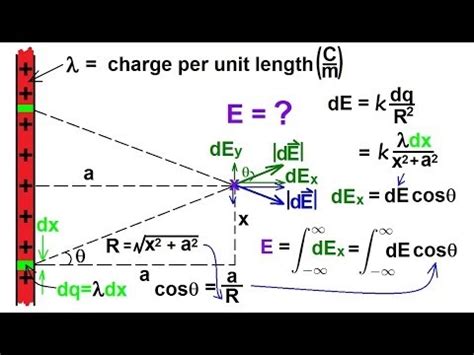
Table of Contents
Electric Field for an Infinite Line of Charge: A Comprehensive Guide
The concept of the electric field generated by an infinite line of charge is a cornerstone in electromagnetism, offering a crucial stepping stone to understanding more complex charge distributions. While a truly infinite line of charge is a theoretical construct, it serves as an excellent approximation for scenarios involving long, thin, uniformly charged conductors. This comprehensive guide delves into the derivation, implications, and applications of the electric field produced by such a line charge.
Understanding the Problem: Infinite Line of Charge
Imagine a long, straight line carrying a uniform linear charge density, λ (lambda), measured in Coulombs per meter (C/m). This means that every meter of the line carries the same amount of charge. The challenge is to determine the electric field at any point in space due to this infinite distribution of charge. We'll use Gauss's Law, a powerful tool in electromagnetism, to elegantly solve this problem.
Why Gauss's Law?
Directly calculating the electric field using Coulomb's Law for an infinite number of infinitesimal charges would be incredibly complex, bordering on impossible. Gauss's Law provides a shortcut, relating the electric flux through a closed surface to the enclosed charge. The key is choosing the right Gaussian surface – a surface that simplifies the calculation.
Applying Gauss's Law: Choosing the Gaussian Surface
The symmetry of the problem dictates our choice of Gaussian surface. Since the line charge is infinitely long and uniformly charged, the electric field will be radially symmetric, pointing directly away from the line (for a positive charge density). Therefore, a cylindrical Gaussian surface is the ideal choice.
Consider a cylindrical Gaussian surface of radius r and length L, with its axis coinciding with the infinite line charge. The surface consists of three parts:
- Curved Surface: The lateral surface of the cylinder.
- End Caps: The two circular ends of the cylinder.
Why a Cylinder?
The cylindrical symmetry ensures that the electric field is perpendicular to the curved surface at every point. This simplifies the calculation of the electric flux through this surface. The flux through the end caps is zero because the electric field is parallel to these surfaces.
Calculating the Electric Flux
Gauss's Law states:
∮ E • dA = Q<sub>enc</sub> / ε₀
where:
- E is the electric field vector.
- dA is a vector element of the Gaussian surface area, pointing outward.
- Q<sub>enc</sub> is the total charge enclosed within the Gaussian surface.
- ε₀ is the permittivity of free space (8.854 x 10<sup>-12</sup> C²/Nm²).
Let's break down the flux calculation:
-
Flux through the curved surface: The electric field is constant in magnitude and perpendicular to the curved surface. Therefore, the flux through this surface is simply E * A<sub>curved</sub> = E * (2πrL), where A<sub>curved</sub> is the area of the curved surface.
-
Flux through the end caps: The electric field is parallel to the end caps, meaning the angle between E and dA is 90°. Consequently, the flux through the end caps is zero (E • dA = 0).
Therefore, the total flux through the Gaussian surface is:
∮ E • dA = E * (2πrL)
Calculating the Enclosed Charge
The total charge enclosed within the Gaussian surface is simply the linear charge density multiplied by the length of the cylinder:
Q<sub>enc</sub> = λL
Solving for the Electric Field
Substituting the expressions for the flux and enclosed charge into Gauss's Law, we get:
E * (2πrL) = λL / ε₀
Solving for the electric field E:
E = λ / (2πε₀r)
This equation represents the magnitude of the electric field at a distance r from the infinite line of charge. The direction of the electric field is radially outward if λ is positive and radially inward if λ is negative.
Implications and Interpretations of the Result
The inverse relationship between the electric field strength (E) and the distance (r) is crucial. The electric field weakens as you move further away from the line charge, decreasing proportionally to 1/r. This is significantly different from the 1/r² dependence observed in the electric field of a point charge.
Key Observations:
-
Radial Symmetry: The electric field is directed radially outward (or inward for a negative line charge). This is a direct consequence of the cylindrical symmetry of the problem.
-
Inverse Proportionality: The field strength is inversely proportional to the distance from the line charge. This means doubling the distance reduces the field strength by half.
-
Independence of Length: The length L of the Gaussian cylinder cancels out in the final equation, highlighting the fact that the electric field is independent of the length considered along the infinite line charge. This reinforces the theoretical nature of the "infinite" line charge model.
Applications of the Infinite Line Charge Model
While a perfectly infinite line charge doesn't exist in reality, this model offers valuable approximations for several practical scenarios:
-
Long, Thin Conductors: The electric field near a long, thin, uniformly charged conductor can be well-approximated using the infinite line charge model. This is particularly useful for analyzing the field near transmission lines, coaxial cables, and other similar structures.
-
Cylindrical Capacitors: The model plays a role in determining the capacitance of cylindrical capacitors.
-
Electrostatic Problems: In many electrostatic problems involving long, slender objects, the infinite line charge model provides a simplified but reasonably accurate calculation of the electric field, reducing complex integration problems to a straightforward formula.
-
Ion Beams and Electron Beams: The model can be used to approximately represent the electric field generated by long beams of charged particles.
Limitations and Refinements of the Model
The infinite line charge model, while useful, has limitations:
-
Idealization: The concept of an infinite line charge is an idealization. Real-world conductors have finite lengths, and the charge distribution might not be perfectly uniform.
-
Near-End Effects: The model becomes less accurate near the ends of a finite conductor, where the cylindrical symmetry breaks down.
-
Charge Distribution: In reality, the charge distribution on a conductor may not be uniform, especially if there are nearby conductors or other electric fields present.
These limitations should be considered when applying the infinite line charge model to real-world problems. For more accurate results in cases where the limitations are significant, numerical methods or more complex analytical models may be needed.
Advanced Concepts and Further Exploration
The concept of the electric field for an infinite line of charge can be extended and explored further:
-
Superposition Principle: The electric field due to multiple infinite line charges can be calculated by applying the superposition principle, adding the electric fields generated by each line charge individually. This approach helps address scenarios with more complex charge distributions.
-
Potential Difference: Calculating the potential difference between two points in the electric field generated by the infinite line charge leads to a logarithmic dependence, providing further insight into the potential energy associated with this field.
-
Electric Field Energy Density: This field presents an opportunity to explore the energy density associated with the electric field, leading to a deeper understanding of energy storage and distribution in electrostatic systems.
Conclusion
The electric field for an infinite line of charge, while a theoretical construct, serves as an invaluable tool in electromagnetism. Its derivation using Gauss's Law exemplifies the power and elegance of this fundamental law. Understanding this model provides a strong foundation for tackling more complex charge distributions and exploring various applications in electrostatics and beyond. The inverse proportionality to distance, the radial symmetry, and the independence of the solution from the length of the Gaussian cylinder are all crucial aspects of this model's characteristics and applications. By carefully understanding both its strengths and limitations, this model can be a powerful tool for solving many real-world problems with impressive accuracy. Remember to always consider the context and limitations to ensure the accuracy and relevance of your calculations.
Latest Posts
Latest Posts
-
Rank The Compounds Below In Order Of Decreasing Base Strength
Apr 03, 2025
-
Which Is A Sign Of Reproductive Maturity
Apr 03, 2025
-
What Is The Difference Between Large And Small Scale Maps
Apr 03, 2025
-
1 Atomic Mass Unit Is Equal To
Apr 03, 2025
-
Oxidation Number Of Carbon In Co
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Electric Field For Infinite Line Of Charge . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
