E To The What Equals 0
News Leon
May 03, 2025 · 5 min read
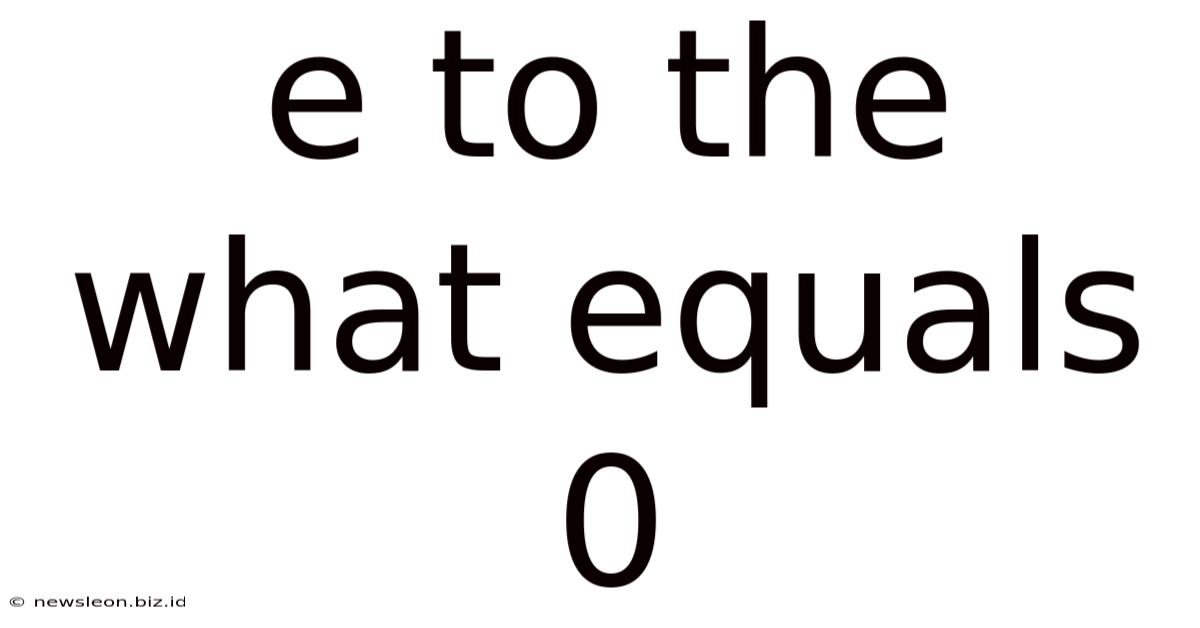
Table of Contents
e to the what equals 0? Exploring the Solution to eˣ = 0
The equation eˣ = 0 is a deceptively simple-looking problem in mathematics. It's a question that often arises in calculus, exponential functions, and complex analysis. While seemingly straightforward, understanding its solution requires a deeper dive into the properties of the exponential function and the nature of complex numbers. This comprehensive article will explore the solution, delve into the reasoning behind it, and touch upon relevant mathematical concepts.
Understanding the Exponential Function, eˣ
Before we tackle the equation eˣ = 0, it's crucial to establish a strong understanding of the exponential function eˣ. This function, where e is Euler's number (approximately 2.71828), represents continuous exponential growth. Several key properties define this function:
-
Always Positive: For any real number x, eˣ is always positive. This is a fundamental characteristic. The graph of y = eˣ never touches or crosses the x-axis.
-
Monotonic Increase: As x increases, eˣ also increases monotonically. There are no peaks or valleys in its curve; it steadily rises.
-
Inverse Function: Natural Logarithm (ln x): The inverse function of eˣ is the natural logarithm, ln x. This means that if eˣ = y, then x = ln y.
-
Derivative and Integral: The derivative of eˣ is eˣ itself, a unique property among functions. Its integral is also eˣ plus a constant of integration.
These properties collectively highlight the inherent nature of eˣ: it's a function that always yields positive values and continuously grows without bound.
Why eˣ = 0 Has No Real Solution
Given the properties discussed above, it becomes clear why the equation eˣ = 0 has no real solution. As we've established, eˣ is always positive for any real value of x. Therefore, it can never equal zero. There is no real number x that, when plugged into the equation, results in zero. Trying to solve it using the natural logarithm would lead to x = ln(0), which is undefined for real numbers. The natural logarithm is only defined for positive values.
Exploring the Complex Plane: A Potential Solution?
While there's no real solution, the landscape changes when we consider complex numbers. Complex numbers extend the real number system by including an imaginary unit, i, defined as the square root of -1. A complex number is typically expressed in the form a + bi, where a and b are real numbers.
In the complex plane, Euler's formula provides a powerful connection between exponential functions and trigonometric functions:
e^(ix) = cos(x) + i sin(x)
This formula opens the door to exploring solutions for eˣ = 0 in the complex domain. However, even with Euler's formula, finding a direct solution remains elusive. The exponential function, even in the complex plane, maintains a fundamental property: its magnitude is always positive.
Magnitude and Argument in the Complex Plane
When dealing with complex numbers, we often refer to their magnitude (or modulus) and argument (or phase). The magnitude of a complex number z = a + bi is represented as |z| and calculated as √(a² + b²). The argument is the angle θ such that z = |z|(cos θ + i sin θ).
Let's consider eˣ where x is a complex number, say x = a + bi. Then, eˣ = e^(a+bi) = eᵃ * e^(bi). Using Euler's formula, we have:
eˣ = eᵃ * (cos(b) + i sin(b))
The magnitude of eˣ is |eˣ| = |eᵃ| * |cos(b) + i sin(b)| = eᵃ. Since eᵃ is always positive for any real number a, the magnitude of eˣ will always be positive. Therefore, even in the complex plane, |eˣ| ≠ 0.
The Limit as x Approaches Negative Infinity
While there's no solution where eˣ equals exactly zero, we can consider the limit of eˣ as x approaches negative infinity:
lim (x→-∞) eˣ = 0
This means that as x becomes increasingly negative, the value of eˣ approaches zero arbitrarily closely. However, it never actually reaches zero. This limit is often used in calculus and analysis to deal with situations where eˣ is vanishingly small.
Implications and Applications
The fact that eˣ = 0 has no solution is not a trivial matter. It has profound implications across various areas of mathematics and science. For instance:
-
Differential Equations: Many differential equations involve the exponential function. The absence of a solution to eˣ = 0 influences the behavior of solutions to these equations and the conditions for their existence.
-
Probability and Statistics: The exponential distribution, widely used in probability and statistics, is related to the exponential function. Understanding the behavior of eˣ is critical in analyzing and interpreting data from exponential distributions.
-
Signal Processing: The exponential function plays a critical role in signal processing, particularly in analyzing decaying signals. The understanding of its behavior near zero is fundamental.
-
Financial Modeling: Exponential functions are frequently used in financial models for compound interest and growth. The absence of a zero solution indicates that even with negative growth rates (represented by negative values of x), the value will never become zero, although it may approach it asymptotically.
Conclusion: A Deep Dive into a Seemingly Simple Equation
The seemingly simple equation eˣ = 0 unveils a wealth of insights into the nature of exponential functions, complex numbers, and their applications. While it possesses no solution in the real or complex number systems, understanding why it has no solution, exploring the limiting behavior as x approaches negative infinity, and grasping the implications for various mathematical fields enriches our understanding of advanced mathematical concepts. The journey to understanding this equation leads us down a path of exploring the rich interconnectedness of different mathematical domains, emphasizing the importance of rigorous mathematical thinking and analysis. The pursuit of understanding this seemingly simple equation has led us to a much deeper appreciation of the profound properties of the exponential function within the real and complex number systems.
Latest Posts
Related Post
Thank you for visiting our website which covers about E To The What Equals 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.