Draw A Line Segment Of 7.2 Cm And Bisect It
News Leon
Apr 03, 2025 · 5 min read
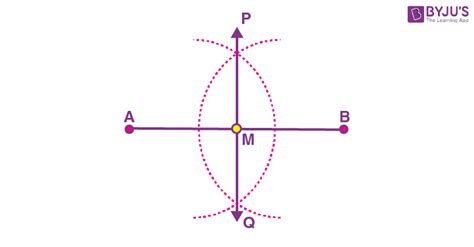
Table of Contents
Draw a Line Segment of 7.2 cm and Bisect It: A Comprehensive Guide
Constructing accurate geometric figures is a fundamental skill in mathematics and various practical applications. This guide provides a detailed explanation of how to draw a line segment of 7.2 cm and bisect it using both compass and ruler methods, alongside discussions of the underlying geometric principles and practical applications.
Understanding Line Segments and Bisection
Before we delve into the construction process, let's clarify some fundamental geometric terms:
Line Segment: A line segment is a part of a line that is bounded by two distinct end points. It has a definite length. In our case, we'll be constructing a line segment of 7.2 cm.
Bisection: Bisection means dividing something into two equal parts. In geometry, bisecting a line segment means finding the midpoint that divides the segment into two equal halves.
Method 1: Bisecting a Line Segment Using a Ruler and Compass
This is the classic and most accurate method for bisecting a line segment. It relies on the properties of circles and their intersections.
Step 1: Draw the Line Segment
- Using a ruler, carefully draw a straight line segment of 7.2 cm. Mark the endpoints as A and B. Accuracy is crucial here; a precise measurement is vital for accurate bisection. Make sure your pencil is sharpened to create a clear, thin line.
Step 2: Constructing Arcs
-
Place the compass point at point A. Adjust the compass width to slightly more than half the length of the line segment (a radius greater than 3.6 cm). Draw an arc above and below the line segment. The arc should extend sufficiently to create clear intersection points later. Make sure the compass width remains consistent throughout this step.
-
Without changing the compass width, place the compass point at point B. Draw two more arcs, one above and one below the line segment, ensuring they intersect the arcs drawn in the previous step. This creates two pairs of intersecting arcs. Observe how the intersection points are equidistant from points A and B.
Step 3: Drawing the Bisector
- Use your ruler to draw a straight line connecting the two upper intersection points of the arcs. Then, draw a line connecting the two lower intersection points. You will notice that both lines pass through the same point on the original line segment AB. This is the midpoint of the line segment. This point perfectly bisects the line segment into two equal halves of 3.6 cm each.
Step 4: Verification
- Measure each half of the bisected line segment using your ruler. Both segments should measure exactly 3.6 cm. If there's a slight discrepancy, it may be due to minor inaccuracies in the construction process or the tools used. It is acceptable to have minimal differences within the acceptable margin of error.
Method 2: Bisecting a Line Segment Using a Ruler Only (Approximate Method)
This method is simpler but provides only an approximate bisection. It's suitable when high precision is not required.
Step 1: Measure the Line Segment
- Using a ruler, measure the length of the line segment (7.2 cm).
Step 2: Find the Midpoint
- Divide the total length of the line segment by 2 (7.2 cm / 2 = 3.6 cm).
Step 3: Mark the Midpoint
- Using your ruler, carefully mark a point on the line segment that is exactly 3.6 cm from either endpoint. This point represents the approximate midpoint of the line segment.
Step 4: Verification (Approximate)
- Measure the two segments created by the marked midpoint. They should ideally be approximately 3.6 cm each. Keep in mind this method is less precise than the compass and ruler method.
Geometric Principles Behind Bisection
The compass and ruler method leverages several key geometric principles:
- Circle Properties: The arcs drawn from points A and B are parts of circles with equal radii. The intersection points of these arcs are equidistant from both A and B.
- Perpendicular Bisector: The line connecting the intersection points is the perpendicular bisector of the line segment AB. A perpendicular bisector is a line that intersects another line segment at a right angle (90 degrees) and passes through its midpoint.
Practical Applications of Line Segment Bisection
Bisection of line segments is a fundamental concept with numerous applications in various fields:
- Geometry and Construction: It's crucial in constructing more complex geometric shapes, such as squares, equilateral triangles, and other polygons.
- Engineering and Architecture: Precision is paramount in these fields, and bisecting line segments is essential for accurate blueprints and designs.
- Computer Graphics and CAD: Computer-aided design relies heavily on geometric principles, including the bisection of lines for creating precise models and digital drawings.
- Cartography: Creating accurate maps involves numerous geometric constructions, including line segment bisection, for precise representation of locations and distances.
- Art and Design: The principle of dividing a line into equal parts is useful in creating symmetrical designs and patterns.
Troubleshooting Common Issues
- Inaccurate Measurements: Ensure you use a sharp pencil and ruler for precise measurements. Double-check your measurements at each step.
- Uneven Arcs: Maintain a consistent compass width throughout the process. Too much pressure or variation in compass width can lead to inaccurate intersection points.
- Faulty Line Drawing: Draw thin, straight lines to ensure clear intersections and accurate measurements.
Conclusion
Learning to accurately draw and bisect a line segment is a fundamental skill with wide-ranging applications. The compass and ruler method offers superior precision, while the ruler-only method offers a simplified, approximate solution. Understanding the underlying geometric principles enhances the learning process and fosters a deeper appreciation for geometric constructions. Mastering these techniques enhances problem-solving skills and lays a solid foundation for more advanced geometric explorations. Remember that practice is key to improving accuracy and speed. Keep practicing, and you'll soon be proficient in bisecting line segments with ease.
Latest Posts
Latest Posts
-
Do Plane Mirrors Form Real Images
Apr 03, 2025
-
After 1880 European Colonization Was Motivated By The
Apr 03, 2025
-
Gaps Or Interruptions In The Myelin Sheath Are Called
Apr 03, 2025
-
Some Bacteria Have Small Extrachromosomal Pieces Of Circular Dna Called
Apr 03, 2025
-
How To Calculate The Bandwidth Of A Signal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Draw A Line Segment Of 7.2 Cm And Bisect It . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
