Derivative Of Log Base 3 Of X
News Leon
Apr 07, 2025 · 4 min read
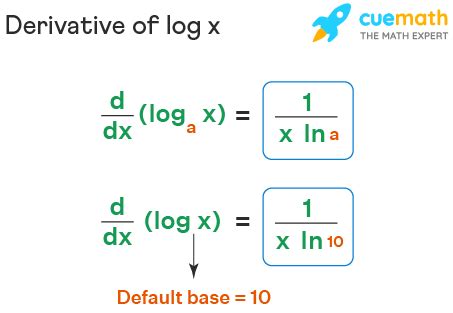
Table of Contents
Derivative of Log Base 3 of x: A Comprehensive Guide
The derivative of a logarithmic function is a fundamental concept in calculus with wide-ranging applications in various fields. This comprehensive guide delves into the process of finding the derivative of log base 3 of x, providing a detailed explanation with examples and addressing common misconceptions. We'll explore different approaches, highlighting the underlying principles and emphasizing the practical applications of this concept.
Understanding Logarithms and Their Derivatives
Before diving into the specific case of log base 3 of x, let's establish a solid foundation. The logarithm of a number to a given base is the exponent to which the base must be raised to produce that number. For example, if we have log₃(x) = y, this means 3ʸ = x.
The derivative of a function measures its instantaneous rate of change. Finding the derivative of a logarithmic function involves applying the rules of differentiation, specifically the chain rule and the derivative of the natural logarithm (ln x). The natural logarithm, with base e (Euler's number, approximately 2.718), holds a special place in calculus because its derivative is exceptionally simple.
The Derivative of ln x
The derivative of the natural logarithm of x is:
d/dx (ln x) = 1/x
This simple form is crucial in deriving the derivatives of logarithms with other bases.
Change of Base Formula: The Key to Solving Log₃(x)
The key to finding the derivative of log₃(x) lies in the change of base formula for logarithms. This formula allows us to convert a logarithm from one base to another. The general formula is:
logₐ(b) = logₓ(b) / logₓ(a)
Where 'a' is the original base, 'b' is the argument, and 'x' is the new base. We typically use either base 10 or base e (natural logarithm) for calculations.
Deriving the Derivative of log₃(x)
Let's use the change of base formula to rewrite log₃(x) in terms of the natural logarithm:
log₃(x) = ln(x) / ln(3)
Notice that ln(3) is a constant. Now, we can apply the rules of differentiation. Specifically, we'll use the constant multiple rule, which states that the derivative of a constant times a function is the constant times the derivative of the function:
d/dx [c * f(x)] = c * d/dx [f(x)]
Applying this rule to our equation:
d/dx [log₃(x)] = d/dx [ln(x) / ln(3)]
Since 1/ln(3) is a constant, we can pull it out:
d/dx [log₃(x)] = (1/ln(3)) * d/dx [ln(x)]
Now, we know the derivative of ln(x) is 1/x. Substituting this, we get:
d/dx [log₃(x)] = (1/ln(3)) * (1/x)
Therefore, the derivative of log base 3 of x is:
d/dx [log₃(x)] = 1 / (x * ln(3))
Illustrative Examples
Let's solidify our understanding with a few examples:
Example 1: Find the derivative of f(x) = log₃(x²)
First, we use the logarithm power rule: log₃(x²) = 2log₃(x)
Then, we differentiate:
f'(x) = 2 * d/dx[log₃(x)] = 2 * [1 / (x * ln(3))] = 2 / (x * ln(3))
Example 2: Find the derivative of f(x) = x²log₃(x)
Here, we'll need to use the product rule: d/dx[u(x)v(x)] = u'(x)v(x) + u(x)v'(x)
Let u(x) = x² and v(x) = log₃(x)
u'(x) = 2x v'(x) = 1 / (x * ln(3))
Applying the product rule:
f'(x) = (2x)log₃(x) + x²(1 / (x * ln(3))) = 2xlog₃(x) + x / ln(3)
Applications of the Derivative of Logarithmic Functions
The derivative of logarithmic functions, including log₃(x), has diverse applications across many fields:
- Economics: Analyzing growth rates in economic models, particularly those involving exponential growth or decay.
- Physics: Modeling radioactive decay, population growth, and other processes involving exponential change. The derivative helps determine the rate of change at any given point in time.
- Computer Science: Analyzing algorithms' efficiency and complexity. Logarithmic functions often describe the time complexity of efficient search algorithms.
- Finance: Calculating continuous compound interest rates and determining the rate of change of investment values.
- Statistics: Working with logarithmic transformations of data, particularly in cases of skewed distributions. The derivative helps in understanding how changes in the original data affect the transformed data.
Addressing Common Misconceptions
- Confusing the derivative with the integral: The derivative and integral are inverse operations. While the derivative measures the rate of change, the integral calculates the area under a curve.
- Forgetting the chain rule: When differentiating composite logarithmic functions, remember to apply the chain rule.
- Incorrectly applying the power rule: The power rule of differentiation does not apply directly to logarithmic functions.
Conclusion
The derivative of log base 3 of x, 1 / (x * ln(3)), is a valuable tool in calculus and its applications. By understanding the change of base formula and applying the rules of differentiation correctly, one can confidently solve problems involving this logarithmic function. Remember to consider the chain rule when dealing with composite functions. This comprehensive guide provides a robust foundation for understanding and applying this important concept in various mathematical and scientific contexts. Mastering this concept will unlock a deeper understanding of calculus and its profound impact on different fields. The applications are vast and the possibilities are endless! Practice makes perfect; so continue practicing and exploring different problems to strengthen your understanding.
Latest Posts
Latest Posts
-
Having Two Identical Alleles For A Trait
Apr 08, 2025
-
Is Grain Farming Commercial Or Subsistence
Apr 08, 2025
-
Composed Mostly Of Carbon Hydrogen And Oxygen
Apr 08, 2025
-
What Fraction Is Represented By Point A
Apr 08, 2025
-
Can A Substance Contract On Heating Give An Example
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of Log Base 3 Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.