A Triangle Has 3 Equal Sides
News Leon
Mar 30, 2025 · 6 min read
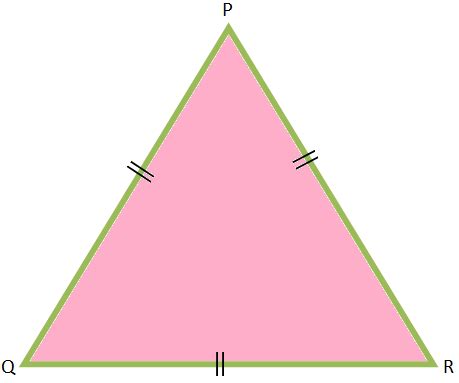
Table of Contents
A Triangle Has 3 Equal Sides: Exploring the Equilateral Triangle
An equilateral triangle, a cornerstone of geometry, is defined by its three equal sides. This seemingly simple characteristic unlocks a world of fascinating properties and applications, extending far beyond the basic principles of geometry. This exploration will delve deep into the characteristics, calculations, and applications of this fundamental geometric shape.
Defining the Equilateral Triangle
An equilateral triangle is a polygon, specifically a triangle, with all three sides of equal length. This equality of sides inherently dictates other crucial properties, including the equality of its angles. Each interior angle of an equilateral triangle measures exactly 60 degrees. This consistent angular measurement is a direct consequence of the equal side lengths. The symmetry inherent in this structure is a key aspect that makes it so useful in various fields.
Key Characteristics:
- Three Equal Sides: The defining characteristic – all sides possess identical length.
- Three Equal Angles: Each interior angle measures 60 degrees. This makes it an equiangular triangle as well.
- Symmetry: It possesses three lines of symmetry, each bisecting an angle and the opposite side.
- Regular Polygon: It is the simplest example of a regular polygon – a polygon with all sides and angles equal.
Calculating Properties of an Equilateral Triangle
Understanding how to calculate various properties of an equilateral triangle is essential for its application in various contexts. These calculations rely heavily on the relationship between its sides, angles, and altitude.
Calculating the Perimeter:
The perimeter of any polygon is simply the sum of the lengths of its sides. Given the equilateral triangle's equal sides, the perimeter calculation is straightforward:
Perimeter = 3 * side length
For example, if the side length is 5 cm, the perimeter is 3 * 5 cm = 15 cm.
Calculating the Area:
The area of an equilateral triangle can be calculated in a few ways. The most common formula utilizes the side length:
Area = (√3 / 4) * side length²
Alternatively, if the height (altitude) is known, a simpler formula can be used:
Area = (1/2) * base * height
where the base is one of the sides of the triangle. The height can be calculated using the Pythagorean theorem, as detailed in the next section.
Calculating the Height (Altitude):
The height, or altitude, of an equilateral triangle is the perpendicular distance from a vertex to the opposite side. It bisects both the angle at the vertex and the opposite side. Using the Pythagorean theorem, we can derive the formula:
Height = (√3 / 2) * side length
This formula elegantly connects the height to the side length, highlighting the inherent proportionality within the equilateral triangle.
Calculating the Radius of the Inscribed and Circumscribed Circles:
An inscribed circle is the largest circle that can fit inside the triangle, touching all three sides. A circumscribed circle passes through all three vertices. The radii of these circles are related to the side length:
- Radius of Inscribed Circle (inradius): (√3 / 6) * side length
- Radius of Circumscribed Circle (circumradius): (1/√3) * side length
These radii play crucial roles in various geometrical constructions and calculations.
The Equilateral Triangle in Geometry and Mathematics
The equilateral triangle's unique properties make it a fundamental building block in various areas of geometry and mathematics.
Tessellations and Geometry:
Equilateral triangles can perfectly tessellate (tile a plane without gaps or overlaps), forming regular hexagonal patterns. This ability to create a seamless tiling pattern is crucial in various design applications, from mosaics to honeycomb structures in nature. Understanding these tessellations reveals deeper insights into geometric packing and space-filling.
Trigonometry and Angle Relationships:
The 60-degree angles of an equilateral triangle are essential in trigonometry. They are fundamental angles that allow for the derivation of trigonometric ratios and identities. The inherent symmetry simplifies calculations and aids in understanding trigonometric functions.
Advanced Geometric Constructions:
Equilateral triangles are used in various advanced geometric constructions, including creating regular hexagons and other geometric figures. Their predictable properties make them ideal tools for constructing more complex shapes with precision.
Fractals and Self-Similarity:
The equilateral triangle's symmetry leads to fascinating applications in fractal geometry. By recursively dividing an equilateral triangle into smaller similar triangles, one can generate intricate and self-similar fractal patterns, showcasing the beauty and complexity hidden within simple geometric shapes.
Real-World Applications of the Equilateral Triangle
The equilateral triangle's unique properties extend beyond the purely theoretical, finding practical applications across various fields.
Architecture and Engineering:
The inherent stability and symmetry of equilateral triangles make them popular in architecture and engineering. They are frequently used in structural designs, ensuring strength and stability in bridges, buildings, and other constructions. Their ability to distribute weight evenly makes them ideal for supporting loads.
Design and Art:
The aesthetic appeal of equilateral triangles is evident in various design and art forms. Their symmetry and balance are employed in logos, patterns, and artistic compositions to create visually pleasing designs. Their geometric simplicity yet inherent elegance makes them versatile design elements.
Nature and Biology:
Equilateral triangles appear unexpectedly in nature. The hexagonal structure of honeycombs is directly related to the tessellation properties of equilateral triangles. Many crystalline structures also exhibit triangular symmetries, demonstrating the triangle's importance in natural formations.
Computer Graphics and Game Development:
In computer graphics and game development, equilateral triangles are used in polygon modelling, creating realistic textures, and defining the geometry of objects. Their simple geometry allows for efficient processing and rendering.
Beyond the Basics: Exploring Further Properties
While we’ve covered fundamental properties, there's more to explore regarding equilateral triangles.
Centroids, Orthocenters, and Circumcenters:
In an equilateral triangle, the centroid (intersection of medians), orthocenter (intersection of altitudes), and circumcenter (intersection of perpendicular bisectors) all coincide at a single point. This unique property highlights the triangle's exceptional symmetry.
Area Calculations using Trigonometry:
The area can also be calculated using trigonometry: (1/2)ab sin(C), where a and b are two sides, and C is the included angle. In the equilateral triangle, this simplifies to (√3/4)a², confirming the previous area formula.
Relationship to Other Geometric Shapes:
Equilateral triangles are intimately related to other shapes like hexagons, tetrahedrons, and other regular polygons. Understanding these connections provides a deeper appreciation for geometric relationships.
Conclusion: The Enduring Significance of the Equilateral Triangle
The equilateral triangle, with its seemingly simple definition, holds a surprising depth and complexity. Its inherent symmetry, predictable properties, and diverse applications across numerous fields cement its position as a fundamental geometric shape. From tessellations in nature to structural designs in engineering, the equilateral triangle continues to inspire and inform, demonstrating the profound beauty and practical utility hidden within a basic geometric form. Its exploration never truly ends, as mathematicians and scientists continue to uncover new facets of its elegance and power. The equilateral triangle remains a powerful example of how seemingly simple elements can lead to profound understanding and application across many fields of study.
Latest Posts
Latest Posts
-
Which Of The Following Is True Of B Cells
Apr 01, 2025
-
How Many Parents Are Involved In Asexual Reproduction
Apr 01, 2025
-
What Is The Order Of The Breakdown Products Of Hemoglobin
Apr 01, 2025
-
What Muscle Subdivides The Ventral Body Cavity
Apr 01, 2025
-
How Do You Separate Iron Filings And Sand
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about A Triangle Has 3 Equal Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
