A Rectangle Is A Parallelogram With A Right Interior Angle
News Leon
Apr 05, 2025 · 5 min read
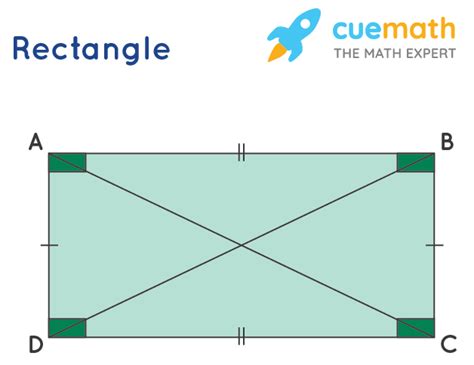
Table of Contents
A Rectangle is a Parallelogram with a Right Interior Angle: A Deep Dive into Geometric Properties
Understanding the relationship between rectangles and parallelograms is fundamental to mastering geometry. This article will thoroughly explore the defining characteristics of both shapes, focusing on why a rectangle is, in fact, a special type of parallelogram distinguished by the presence of a right interior angle. We'll delve into the properties, theorems, and practical applications, providing a comprehensive guide suitable for students and enthusiasts alike.
Parallelograms: The Foundation
Before diving into rectangles, let's establish a solid understanding of parallelograms. A parallelogram is a quadrilateral—a four-sided polygon—with two pairs of parallel sides. This seemingly simple definition leads to several crucial properties:
Key Properties of Parallelograms:
- Opposite sides are parallel and equal in length: This is the defining characteristic. If sides AB and CD are parallel and equal, and sides BC and DA are parallel and equal, then ABCD is a parallelogram.
- Opposite angles are equal: Angles A and C will be equal, as will angles B and D.
- Consecutive angles are supplementary: This means that the sum of any two adjacent angles (e.g., A and B) equals 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at a point that divides each diagonal into two equal segments.
These properties are interconnected and can be used to prove that a given quadrilateral is a parallelogram. For instance, if you can demonstrate that opposite sides are parallel, you automatically know that opposite angles are equal and diagonals bisect each other. This interconnectedness makes parallelograms a powerful building block in geometric reasoning.
Rectangles: A Special Case of Parallelograms
Now, let's introduce the rectangle. A rectangle is a parallelogram with one additional crucial property:
Defining Property of a Rectangle:
- All interior angles are right angles (90 degrees): This single characteristic elevates a parallelogram to the status of a rectangle. Because it's a parallelogram, it inherits all the properties listed above, but the addition of right angles introduces further specific traits.
Consequently, a rectangle possesses all the properties of a parallelogram plus the following:
Additional Properties of Rectangles:
- All angles are equal (90 degrees): This directly follows from the definition.
- Diagonals are equal in length: Unlike a general parallelogram where diagonals can have different lengths, a rectangle's diagonals are always equal. This is a crucial distinguishing feature.
- Diagonals bisect each other: This property, inherited from the parallelogram, implies that the diagonals intersect at their midpoints.
Proving a Rectangle is a Parallelogram
To solidify the relationship, let's demonstrate mathematically why a rectangle is a parallelogram. Consider a rectangle ABCD. We can use the properties of parallel lines and transversals to prove that opposite sides are parallel:
- Angles: Since all interior angles are 90 degrees, we have ∠A = ∠B = ∠C = ∠D = 90°.
- Consecutive Angles: Consider angles A and B. Since ∠A + ∠B = 90° + 90° = 180°, these angles are supplementary. Similarly, ∠B + ∠C = 180°, ∠C + ∠D = 180°, and ∠D + ∠A = 180°.
- Parallel Lines: Supplementary consecutive angles imply that sides AB and CD are parallel, as are sides BC and DA. This is because if two lines are intersected by a transversal and consecutive interior angles are supplementary, then the lines are parallel (a theorem of parallel lines).
- Parallelogram: Since opposite sides are parallel, ABCD satisfies the definition of a parallelogram.
Therefore, we've rigorously shown that a rectangle, by its inherent properties, is a parallelogram.
Visualizing the Relationship
Imagine a parallelogram. You can visualize it as a slanted box. Now, imagine gradually "straightening" the parallelogram, making its angles closer to 90 degrees. As the angles approach 90 degrees, the slanted sides become more perpendicular, and the parallelogram transforms into a rectangle—a perfectly squared-off, upright box. This visual representation reinforces the idea that a rectangle is a specific, more constrained version of a parallelogram.
Practical Applications and Examples
The properties of rectangles are extensively used in various fields:
- Construction and Architecture: Rectangles form the basis of building designs, from the walls and floors of houses to the frames of windows and doors. The stability and predictability of rectangular shapes make them ideal for structural purposes.
- Engineering: Rectangular structures are used in bridges, roads, and many other engineering projects due to their strength and ease of construction.
- Graphic Design: Rectangles are frequently used in graphic design to create layouts, frames, and other visual elements.
- Everyday Objects: Countless everyday objects are rectangular, from books and television screens to tables and doors.
Distinguishing Rectangles from Other Quadrilaterals
It's essential to differentiate rectangles from other quadrilaterals:
- Square: A square is a special type of rectangle where all sides are equal in length. Therefore, a square is a rectangle, but not all rectangles are squares.
- Rhombus: A rhombus is a parallelogram with all sides equal in length. While a rhombus has equal sides, its angles are not necessarily 90 degrees, unlike a rectangle.
- Trapezoid: A trapezoid has only one pair of parallel sides, unlike parallelograms and rectangles which have two.
Advanced Concepts and Theorems
Several advanced geometric theorems and concepts relate directly to rectangles:
- Pythagorean Theorem: The Pythagorean theorem is particularly relevant to rectangles due to their right angles. In a rectangle, the diagonal forms the hypotenuse of a right-angled triangle, allowing for the calculation of diagonal length using the lengths of the sides.
- Area and Perimeter Calculations: The area of a rectangle (A = length x width) is a straightforward calculation, facilitating practical applications in diverse fields. Similarly, the perimeter is easily calculated.
- Coordinate Geometry: Rectangles can be easily represented and manipulated using coordinate geometry.
Conclusion: A Fundamental Geometric Relationship
The relationship between rectangles and parallelograms is a cornerstone of geometry. Understanding that a rectangle is a specialized parallelogram, inheriting all its properties while adding the critical right-angle condition, is crucial for problem-solving and advanced mathematical study. This comprehensive exploration of their properties, theorems, and applications underscores their importance in both theoretical mathematics and practical applications across numerous fields. The ability to identify and utilize the unique characteristics of rectangles provides a powerful tool for solving geometric problems and understanding the world around us.
Latest Posts
Latest Posts
-
Why Are Maps Important To Geographers
Apr 06, 2025
-
Google Search Console Crawl Reports Let You Monitor
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about A Rectangle Is A Parallelogram With A Right Interior Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
