A Pendulum Consists Of A Small Object
News Leon
Apr 06, 2025 · 6 min read
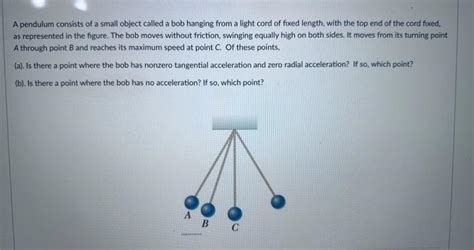
Table of Contents
A Pendulum Consists of a Small Object: Exploring the Physics of Simple Harmonic Motion
The seemingly simple pendulum – a small object suspended from a fixed point by a string or rod – is a cornerstone of classical mechanics. Its rhythmic swing, governed by the immutable laws of physics, has fascinated scientists and thinkers for centuries. From its practical applications in clocks to its role in demonstrating fundamental principles of physics, the pendulum offers a rich field of study. This article delves into the physics behind the pendulum, exploring its motion, the factors influencing its period, and its applications. We'll move beyond the simplistic ideal pendulum to consider the impact of real-world factors like air resistance and the pendulum's physical dimensions.
Understanding Simple Harmonic Motion (SHM)
Before diving into the specifics of the pendulum, it's crucial to understand simple harmonic motion (SHM). SHM is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement. Think of a mass attached to a spring: the farther you pull it, the stronger the spring pulls it back. The pendulum, under certain conditions (which we'll discuss later), exhibits SHM.
Key Characteristics of SHM:
- Period (T): The time taken to complete one full oscillation. This is a constant value for SHM.
- Frequency (f): The number of oscillations per unit time. It's the reciprocal of the period (f = 1/T).
- Amplitude (A): The maximum displacement from the equilibrium position. For small angles, the period of a pendulum is independent of its amplitude.
The Ideal Pendulum: Assumptions and Equations
The theoretical model of an ideal pendulum rests on several simplifying assumptions:
- Massless String or Rod: The string or rod connecting the object to the fixed point has negligible mass compared to the object.
- Point Mass: The object at the end of the string or rod is treated as a point mass, concentrating all its mass at a single point.
- No Air Resistance or Friction: There are no resistive forces acting on the pendulum, meaning its motion is not dampened.
- Small Angle Approximation: The angle of swing is small (typically less than 10 degrees). This assumption allows us to use the small-angle approximation, sin θ ≈ θ (where θ is measured in radians), simplifying the equations of motion.
Under these assumptions, the period (T) of an ideal pendulum is given by the equation:
T = 2π√(L/g)
where:
- L is the length of the string or rod.
- g is the acceleration due to gravity.
This equation reveals a crucial point: the period of an ideal pendulum depends only on the length of the pendulum and the acceleration due to gravity. It is independent of the mass of the object. This is a counter-intuitive but experimentally verifiable fact.
Beyond the Ideal: Real-World Factors
The ideal pendulum is a theoretical construct. In reality, several factors deviate from the ideal model:
1. Air Resistance:
Air resistance acts as a damping force, opposing the motion of the pendulum. Over time, this causes the amplitude of the swing to decrease, eventually bringing the pendulum to rest. The extent of damping depends on factors like the shape and size of the object, the density of the air, and the velocity of the pendulum.
2. Finite Mass of the String or Rod:
In real pendulums, the string or rod has a finite mass. This affects the period, making it slightly longer than predicted by the ideal pendulum equation. More sophisticated equations are required to accurately account for the mass distribution.
3. Large Angle Oscillations:
When the angle of swing is large, the small-angle approximation (sin θ ≈ θ) breaks down. This means the period is no longer independent of the amplitude. The period increases with increasing amplitude in large angle oscillations.
4. Non-uniform Gravity:
The acceleration due to gravity (g) is not uniform across the Earth's surface. It varies with latitude and altitude. This variation slightly affects the pendulum's period, and precise measurements of g can be used to determine the local gravitational field strength.
Applications of Pendulums
Despite their inherent imperfections, pendulums have numerous practical applications:
1. Clocks:
The most well-known application of pendulums is in mechanical clocks. The regular period of a pendulum provides a consistent timekeeping mechanism. Early clocks utilized the pendulum's isochronism (constant period for small angles) to maintain accuracy.
2. Gravity Measurements:
Precise measurements of a pendulum's period can be used to determine the local acceleration due to gravity (g). This is a valuable technique in geophysical surveys, helping to locate underground resources or study variations in the Earth's gravitational field.
3. Seismic Detection:
Sensitive pendulums are used as part of seismometers to detect ground motion caused by earthquakes. The pendulum's inertia resists movement, allowing for the detection of even small seismic waves.
4. Educational Demonstrations:
Pendulums are invaluable tools in physics education, demonstrating fundamental concepts such as SHM, conservation of energy, and the relationship between period and length.
Different Types of Pendulums
Beyond the simple pendulum, several variations exist, each with unique properties:
1. Compound Pendulum:
A compound pendulum consists of an extended rigid body oscillating about a fixed horizontal axis. Its period is more complex to calculate, dependent on the mass distribution of the object.
2. Conical Pendulum:
A conical pendulum is one where the bob moves in a horizontal circle, with the string tracing out a cone. The period depends on the length of the string and the angle of the cone.
3. Physical Pendulum:
A physical pendulum is a more realistic model of a pendulum, considering the mass distribution of the object. The moment of inertia plays a significant role in determining the period.
4. Torsion Pendulum:
A torsion pendulum consists of an object suspended by a thin wire or fiber. The oscillation occurs due to the twisting and untwisting of the wire, with the period dependent on the wire's torsional rigidity and the object's moment of inertia.
Advanced Considerations and Further Research
The study of pendulums extends far beyond the simple equations presented here. Advanced topics include:
- Chaotic Pendulums: When multiple pendulums are coupled or subjected to external forces, chaotic behavior can emerge. This is a fascinating area of research involving complex dynamical systems.
- Damped Pendulums: Detailed mathematical models can account for the effects of air resistance and friction, leading to more accurate predictions of the pendulum's motion.
- Driven Pendulums: The introduction of a driving force can lead to resonance phenomena, where the amplitude of oscillation is significantly amplified at certain frequencies.
The humble pendulum, with its seemingly simple design, offers a rich tapestry of physical phenomena. From its elegant mathematical description to its diverse practical applications, the pendulum continues to inspire research and demonstrate the fundamental principles of classical mechanics. This exploration provides a foundation for deeper investigations into the fascinating world of oscillatory motion. Further research into the advanced topics mentioned above will reveal even greater complexity and subtlety within this seemingly simple system. The pendulum serves as a potent reminder that even seemingly simple systems can hold incredible depth and complexity, continually rewarding those who study its intricate behaviors.
Latest Posts
Latest Posts
-
Area Of Circle With Radius Of 7
Apr 07, 2025
-
Example Of Law Of Conservation Of Charge
Apr 07, 2025
-
Camera Is Input Or Output Device
Apr 07, 2025
-
Molar Mass Of Alum Kal So4 2 12h2o
Apr 07, 2025
-
The Protein Of Hair And Nails Is
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about A Pendulum Consists Of A Small Object . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
