A Chord That Passes Through The Center Of A Circle
News Leon
Apr 01, 2025 · 7 min read
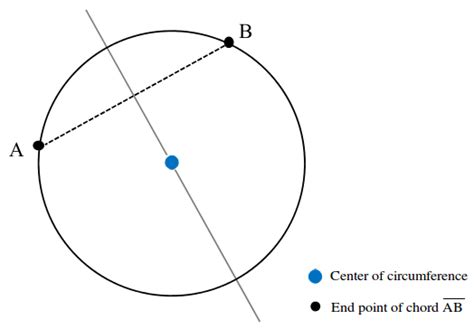
Table of Contents
A Chord That Passes Through the Center of a Circle: Exploring its Unique Properties
A chord is a straight line segment whose endpoints both lie on the circumference of a circle. While seemingly simple, chords hold a wealth of geometric properties, some of which become particularly interesting when the chord passes directly through the center of the circle. This special type of chord, often called a diameter, possesses unique characteristics that are fundamental to understanding circles and their applications in various fields, from engineering and architecture to computer graphics and cartography. This article delves deep into the properties of a chord passing through the center of a circle, exploring its relationship with the radius, circumference, and area of the circle, and highlighting its significance in various mathematical concepts.
Defining the Diameter: The King of Chords
When a chord passes through the center of a circle, it becomes something special: a diameter. The diameter is the longest possible chord in a circle and holds a unique relationship with the radius. The radius, denoted by 'r', is the distance from the center of the circle to any point on its circumference. Crucially, the diameter, denoted by 'd', is precisely twice the length of the radius:
d = 2r
This simple equation encapsulates a fundamental relationship within a circle. Understanding this connection is paramount to solving numerous geometric problems involving circles.
The Diameter and the Circumference: Measuring the Perimeter
The circumference of a circle, denoted by 'C', represents its perimeter – the distance around the circle. The circumference is directly proportional to the diameter, a relationship captured by the famous formula:
C = πd
where 'π' (pi) is a mathematical constant, approximately equal to 3.14159. This formula reveals the fundamental link between the diameter and the overall size of the circle. Knowing the diameter immediately allows us to calculate the circumference and vice-versa. This is crucial in applications requiring the precise measurement of circular objects or spaces. Imagine, for instance, calculating the amount of fencing needed for a circular garden, or determining the length of track needed for a circular running path. In both scenarios, the diameter provides a direct route to calculating the circumference.
Implications of the Circumference Formula:
The formula C = πd elegantly demonstrates the constant ratio between a circle's diameter and its circumference. No matter the size of the circle, this ratio always remains π. This consistent relationship underscores the fundamental properties of circles and contributes significantly to their mathematical elegance and practical usability.
The Diameter and the Area: Enclosing Space
The area of a circle, denoted by 'A', represents the space enclosed within its circumference. The diameter also plays a vital role in calculating the area. While the radius is typically used in the standard area formula:
A = πr²
we can easily substitute the diameter-radius relationship (d = 2r) to obtain an alternative formula expressing area in terms of the diameter:
A = π(d/2)² = (πd²)/4
This alternative formula allows us to calculate the area directly from the diameter measurement, eliminating the need for a separate radius calculation. This is particularly useful when the diameter is the only readily available measurement. For example, consider measuring the area of a circular table whose diameter you can easily measure with a tape measure, but accessing the center point for a direct radius measurement might be difficult.
Area Calculations and Applications:
The ability to calculate the area using either the radius or the diameter is crucial in various practical applications. Consider calculating the surface area of a circular piston, determining the area of a circular crop field, or even estimating the area of a circular swimming pool. The choice of formula depends on the ease of measuring either the radius or the diameter.
The Diameter and Central Angles: Dividing the Circle
A central angle is an angle whose vertex is the center of the circle and whose sides are radii. The diameter plays a crucial role in dividing a circle into sectors. A diameter divides a circle into two equal semicircles, each subtending a central angle of 180 degrees. This property is fundamental in many geometric proofs and constructions.
Sector Area and Arc Length:
Furthermore, knowing the diameter allows for easy calculation of the area of sectors. If we know the central angle of a sector, we can calculate its area as a fraction of the total circle area. Similarly, we can calculate the arc length (the length of the curved part of the sector) using the diameter and the central angle. These calculations are essential in various applications, such as determining the area of a pie slice or calculating the distance traveled along a circular path.
The Diameter and Inscribed Angles: A Deeper Dive
An inscribed angle is an angle formed by two chords that intersect at a point on the circumference. There's a fascinating relationship between inscribed angles and the diameter: if an inscribed angle subtends a diameter (meaning its sides intersect the endpoints of the diameter), it is always a right angle (90 degrees). This property, known as the Thales' theorem, is a cornerstone of geometry and offers a powerful tool for solving various geometric problems.
Thales' Theorem and its Applications:
Thales' theorem has far-reaching implications. It provides a simple and elegant method for constructing right angles using only a compass and straightedge. This is crucial in various geometric constructions, architectural designs, and even in computer graphics where precise angle constructions are essential for rendering shapes.
The Diameter in Three Dimensions: Spheres and Great Circles
The concept of a diameter extends beyond two-dimensional circles into the realm of three-dimensional spheres. In a sphere, a diameter is a line segment that passes through the center of the sphere and connects two points on its surface. A great circle is a circle on the surface of a sphere formed by the intersection of the sphere and a plane passing through the center of the sphere. The diameter of the sphere is also the diameter of every great circle.
Great Circles in Geography and Navigation:
Great circles play a critical role in navigation and geography. The shortest distance between two points on the surface of a sphere (like the Earth) is along a great circle. This concept is fundamental to air and sea navigation, where determining the shortest route between two locations is crucial for efficiency and time-saving.
Diameter in Practical Applications: Examples Beyond Geometry
The concept of the diameter and its associated properties is not confined to theoretical geometry. It holds significant relevance in various practical applications:
-
Engineering: Calculating the diameter of pipes, shafts, wheels, and other circular components is crucial for design and manufacturing processes. Understanding the relationship between diameter and other parameters, like area and circumference, is essential for optimizing design, ensuring structural integrity, and preventing failures.
-
Construction: Determining the diameter of columns, pipes, and other circular elements is crucial for structural calculations and ensuring the stability and safety of buildings and infrastructure. Accurate calculations based on diameter are essential for ensuring that buildings meet safety regulations.
-
Manufacturing: Precise measurements of diameters are crucial in manufacturing processes to ensure that parts meet specifications and fit together correctly. Quality control procedures often involve measuring diameters to ensure consistency and accuracy.
-
Computer Graphics: In computer-aided design (CAD) and computer graphics, the diameter is a fundamental parameter for creating and manipulating circular objects. Understanding the properties of the diameter allows for accurate rendering of shapes and smooth animation of circular objects.
-
Astronomy: The diameter of celestial bodies like planets and stars is a fundamental parameter in astronomical measurements and calculations. Determining the diameter of a celestial body provides valuable information about its size, mass, and other physical properties.
-
Medical Imaging: In medical imaging techniques like ultrasound and MRI, the diameter of various organs and structures is frequently measured to diagnose and monitor diseases. Accurate diameter measurements are essential for assessing the size and health of organs.
Conclusion: The Diameter - A Fundamental Concept
The chord that passes through the center of a circle – the diameter – is far more than just a line segment. It is a fundamental concept in geometry that underpins many important calculations and relationships within circles and spheres. From calculating the circumference and area to understanding inscribed angles and great circles, the diameter plays a pivotal role in solving a wide range of geometric problems and has significant implications across various fields of science, engineering, and technology. Its simplicity belies its power and its importance continues to resonate across diverse applications, emphasizing the enduring legacy of this fundamental geometric concept.
Latest Posts
Latest Posts
-
Why Is The Melting Of Ice Not A Chemical Reaction
Apr 03, 2025
-
Why Is Voltmeter Connected In Parallel
Apr 03, 2025
-
Is Ferment A Physical Or Chemical Change
Apr 03, 2025
-
Give An Example Of A Homologous Structure From This Activity
Apr 03, 2025
-
Is Burning A Candle A Physical Or Chemical Change
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about A Chord That Passes Through The Center Of A Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
