9 To The Power Of 3/2
News Leon
Apr 04, 2025 · 5 min read
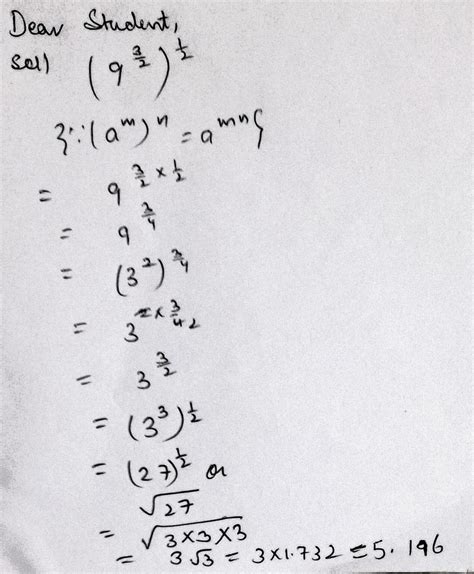
Table of Contents
9 to the Power of 3/2: A Deep Dive into Fractional Exponents
Understanding exponents is fundamental to mathematics, and fractional exponents, in particular, often present a unique challenge for learners. This article provides a comprehensive exploration of 9 to the power of 3/2 (9<sup>3/2</sup>), delving into the underlying principles, various methods of calculation, and practical applications. We'll cover everything from the basic definition of fractional exponents to advanced techniques and real-world examples, ensuring a thorough understanding of this mathematical concept.
Understanding Fractional Exponents
Before tackling 9<sup>3/2</sup>, let's establish a strong foundation in fractional exponents. A fractional exponent, such as 3/2, represents a combination of two operations: exponentiation and root extraction. The numerator (3 in this case) signifies the power to which the base (9) is raised, while the denominator (2) indicates the root to be taken. Therefore, 9<sup>3/2</sup> can be interpreted as the square root of 9 cubed, or (√9)<sup>3</sup>.
Alternatively, it can also be expressed as the cube of the square root of 9, or √(9<sup>3</sup>). Both interpretations yield the same result. This interchangeability is crucial for solving problems involving fractional exponents efficiently. This concept extends to any fractional exponent a/b, where it can be represented as the b-th root of a<sup>a</sup> or (a<sup>a</sup>)<sup>1/b</sup>.
The Importance of the Denominator
The denominator in a fractional exponent is particularly significant. It determines the type of root being extracted. A denominator of 2 indicates a square root, a denominator of 3 indicates a cube root, and so on. Understanding this relationship is paramount to correctly solving problems involving fractional exponents.
The Significance of the Numerator
The numerator in a fractional exponent denotes the power to which the base is raised after the root extraction. It is applied after the root operation is completed. This sequential application of operations (root then power) is a key element in correctly evaluating expressions.
Calculating 9 to the Power of 3/2
Now, let's apply our understanding to calculate 9<sup>3/2</sup>. We can utilize either of the two interpretations mentioned above.
Method 1: (√9)³
- Find the square root of 9: The square root of 9 is 3 (because 3 * 3 = 9).
- Cube the result: 3 cubed (3³) is 3 * 3 * 3 = 27.
Therefore, 9<sup>3/2</sup> = 27.
**Method 2: √(9³) **
- Cube 9: 9 cubed (9³) is 9 * 9 * 9 = 729.
- Find the square root of the result: The square root of 729 is 27 (because 27 * 27 = 729).
Again, we arrive at the same answer: 9<sup>3/2</sup> = 27. This consistency demonstrates the interchangeability of the two methods.
Extending the Concept to Other Numbers
The principles discussed above apply equally to other numbers, not just perfect squares like 9. Let's consider a slightly more complex example, say, 16<sup>3/4</sup>.
Using the equivalent form (a<sup>1/b</sup>)<sup>a</sup>, we first find the fourth root of 16 (which is 2, since 2<sup>4</sup> = 16), and then raise it to the power of 3 (2<sup>3</sup> = 8).
Therefore, 16<sup>3/4</sup> = 8. This highlights the importance of mastering root extraction, as it forms a crucial part of handling fractional exponents. Using a calculator confirms this result, ensuring accuracy and reinforces the concepts.
Dealing with Negative Bases and Fractional Exponents
When dealing with negative bases and fractional exponents, the situation becomes a bit more nuanced. Let's explore the case of (-8)<sup>2/3</sup>. Note the parentheses - they are crucial for indicating that the exponent applies to the entire base, including the negative sign.
Using the method (a<sup>1/b</sup>)<sup>a</sup>, we take the cube root of -8, which is -2. Then, we square this result: (-2)² = 4. Hence, (-8)<sup>2/3</sup> = 4.
However, things become undefined or complex in other scenarios, such as when the denominator is an even number and the base is negative. For instance, (-9)<sup>1/2</sup> is undefined within the realm of real numbers because there's no real number that when multiplied by itself results in -9. This points to the limitations of dealing with even-numbered denominators and negative bases in fractional exponents.
Real-World Applications of Fractional Exponents
Fractional exponents aren't just abstract mathematical concepts; they have numerous applications in various fields:
- Physics: Fractional exponents appear frequently in physics equations, particularly those describing phenomena related to scaling, such as the relationship between the surface area and volume of a sphere.
- Engineering: In engineering, fractional exponents are used in calculations involving stress, strain, and material properties.
- Economics: Growth models in economics frequently employ fractional exponents to represent compounding interest rates or population growth.
- Chemistry: In chemistry, fractional exponents might appear in calculations involving reaction rates or concentration gradients.
- Computer Graphics: In computer graphics, fractional exponents are utilized in creating realistic effects, such as smooth curves and shading.
These are just a few examples, highlighting the wide-ranging utility of fractional exponents in diverse fields.
Advanced Topics and Further Exploration
For those seeking a deeper understanding, exploring these advanced topics can enhance mathematical proficiency:
- Complex Numbers: Extending the concept of fractional exponents to encompass complex numbers unlocks solutions for problems that are undefined in the realm of real numbers.
- Logarithms: Logarithms provide an alternative method for solving equations involving fractional exponents, offering a different perspective and computational approach.
- Calculus: Fractional exponents play a crucial role in differential and integral calculus, particularly when dealing with power functions and their derivatives or integrals.
Conclusion: Mastering Fractional Exponents
Mastering fractional exponents is a critical skill for anyone pursuing studies or careers involving mathematics, science, or engineering. Understanding the underlying principles, exploring different calculation methods, and acknowledging the limitations and extensions of the concept are all vital for successful problem-solving. This comprehensive exploration of 9<sup>3/2</sup> should serve as a solid foundation for tackling more complex fractional exponent problems. Remember the key concepts: the numerator represents the power, the denominator represents the root, and the order of operations matters. By combining these principles with practice, you can confidently tackle any fractional exponent challenge.
Latest Posts
Related Post
Thank you for visiting our website which covers about 9 To The Power Of 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
