8 2 7 As An Improper Fraction
News Leon
Apr 05, 2025 · 5 min read
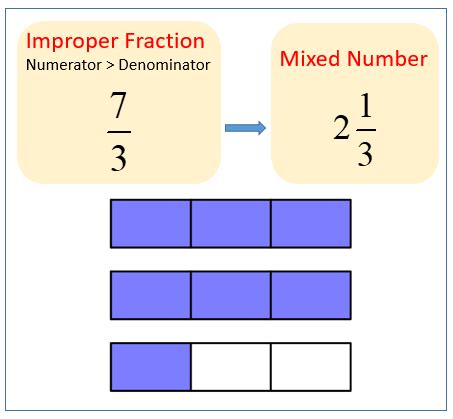
Table of Contents
8 2/7 as an Improper Fraction: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and mastering the conversion between mixed numbers and improper fractions is a crucial skill. This comprehensive guide will delve deep into the process of converting the mixed number 8 2/7 into an improper fraction, explaining the underlying concepts and providing practical examples. We'll also explore the broader context of fractions, their applications, and how this specific conversion might be used in real-world scenarios.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). In our example, 8 2/7, '8' is the whole number, and '2/7' is the proper fraction. This means we have eight whole units and two-sevenths of another unit.
What is an Improper Fraction?
An improper fraction, on the other hand, has a numerator that is greater than or equal to the denominator. This indicates a value greater than or equal to one. Converting a mixed number to an improper fraction essentially represents the entire quantity as a single fraction.
Converting 8 2/7 to an Improper Fraction: The Step-by-Step Process
The conversion process involves two simple steps:
Step 1: Multiply the Whole Number by the Denominator
First, we multiply the whole number (8) by the denominator of the fraction (7):
8 x 7 = 56
This calculation represents the total number of sevenths contained within the eight whole units.
Step 2: Add the Numerator
Next, we add the numerator (2) to the result from Step 1:
56 + 2 = 58
This gives us the total number of sevenths we have in total.
Step 3: Write the Result as an Improper Fraction
Finally, we write the result (58) as the numerator over the original denominator (7):
58/7
Therefore, the improper fraction equivalent of 8 2/7 is 58/7.
Visualizing the Conversion
Imagine you have eight whole pizzas, each cut into seven slices. That's 8 x 7 = 56 slices. You also have two more slices from another pizza. In total, you have 56 + 2 = 58 slices. Since each pizza was cut into seven slices, you have 58/7 slices of pizza in total. This visual representation reinforces the mathematical process.
Why is this Conversion Important?
Converting between mixed numbers and improper fractions is crucial for several reasons:
-
Simplifying Calculations: Improper fractions are often easier to work with when performing addition, subtraction, multiplication, and division of fractions. Working with improper fractions streamlines the process and avoids potential errors.
-
Solving Equations: Many mathematical problems, especially those involving algebra and calculus, require working with fractions. Converting to improper fractions can simplify the solution process significantly.
-
Real-World Applications: Imagine dividing a quantity, like a length of wood or a batch of cookies, into unequal parts. Representing the division as an improper fraction can provide a clearer, more precise representation of the parts involved.
-
Understanding Fraction Relationships: Converting between mixed numbers and improper fractions strengthens your understanding of fraction representation and the relationships between different forms of numerical expression.
Further Exploration of Fractions
Let's explore some additional concepts related to fractions and their conversions:
Reducing Fractions to Lowest Terms
After converting to an improper fraction, it's often beneficial to reduce the fraction to its lowest terms. This means simplifying the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD). In the case of 58/7, the GCD of 58 and 7 is 1, meaning the fraction is already in its simplest form.
Converting Improper Fractions to Mixed Numbers
The reverse process, converting an improper fraction back to a mixed number, involves dividing the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the proper fraction, retaining the original denominator. For example, let's say we have the improper fraction 17/5:
17 ÷ 5 = 3 with a remainder of 2
Therefore, 17/5 is equivalent to the mixed number 3 2/5.
Addition and Subtraction of Fractions
When adding or subtracting fractions, it is often easier to work with improper fractions if the fractions do not have a common denominator. By converting to an improper fraction, we can then find a common denominator and perform the necessary calculations.
Multiplication and Division of Fractions
Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying. Converting mixed numbers to improper fractions before performing these operations simplifies the calculation.
Real-world Examples of Fraction Conversion
Let's examine some practical scenarios where converting 8 2/7 (or similar mixed numbers) to an improper fraction proves useful:
-
Baking: A recipe calls for 8 2/7 cups of flour. To easily calculate the amount of flour needed for a larger batch (e.g., multiplying the recipe by a certain factor), converting 8 2/7 to 58/7 simplifies the multiplication process.
-
Construction: Measuring materials in construction often involves fractions. Converting mixed number measurements to improper fractions can be useful in precise calculations, such as determining the length of materials needed for a project.
-
Finance: Calculating interest or dividing shares often involves fractions. Working with improper fractions can make these calculations clearer and simpler.
-
Science: Many scientific experiments and calculations involve precise measurements, often expressed as fractions. Converting between mixed numbers and improper fractions ensures accurate results.
Conclusion: Mastering Fraction Conversions for Enhanced Mathematical Proficiency
Mastering the conversion of mixed numbers to improper fractions is a cornerstone of mathematical proficiency. Understanding this process, along with the underlying concepts of fractions, enables more efficient and accurate calculations in various contexts. The conversion of 8 2/7 to 58/7 serves as a practical example highlighting the importance of this fundamental skill in both theoretical mathematical exercises and real-world applications across diverse fields. By consistently practicing these conversions and exploring their applications, you’ll strengthen your mathematical foundation and become more confident in solving a wider range of problems. Remember that consistent practice is key to mastering any mathematical concept; so keep practicing, and you’ll soon be comfortable and confident working with fractions of all types.
Latest Posts
Latest Posts
-
At Which Layer Of The Osi Model Do Routers Work
Apr 06, 2025
-
Bangalore Is Capital Of Which State
Apr 06, 2025
-
Cytoplasm Divides Immediately After This Period
Apr 06, 2025
-
What Is The Percent Composition Of Co
Apr 06, 2025
-
In The Visible Spectrum Which Color Has The Longest Wavelength
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 8 2 7 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
