7x 3 - 5x 2 3x
News Leon
May 03, 2025 · 5 min read
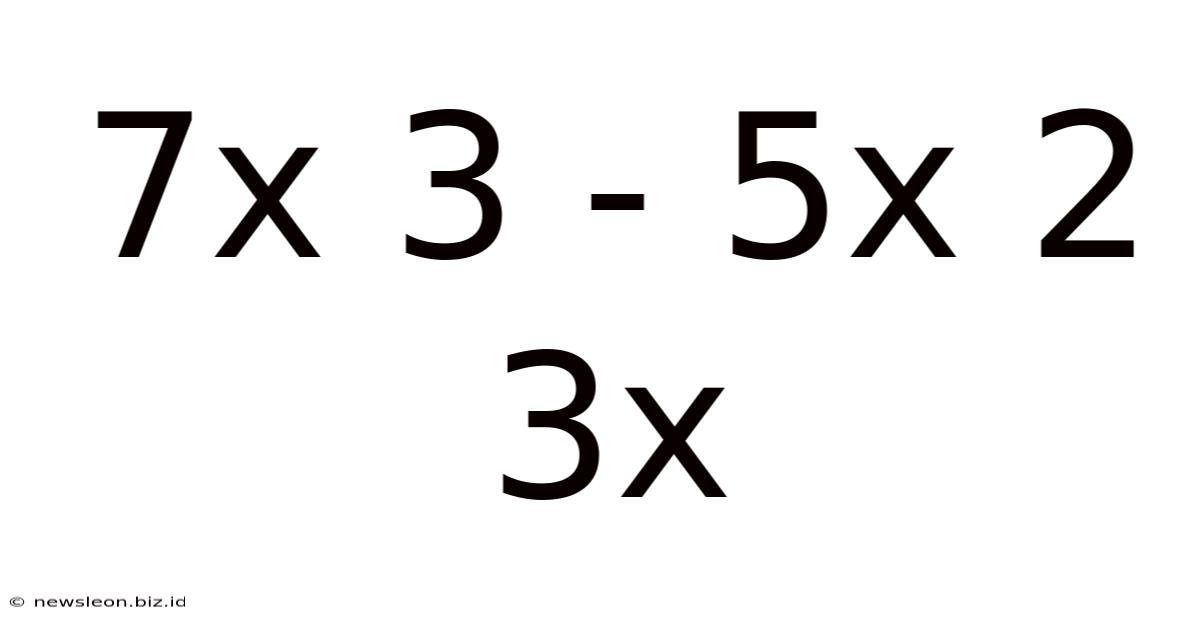
Table of Contents
Decoding the Mathematical Expression: 7x³ - 5x² + 3x
This article delves into the mathematical expression 7x³ - 5x² + 3x, exploring its components, potential applications, and how to approach related problems. We'll cover topics ranging from basic algebraic manipulation to more advanced concepts like finding roots and graphing the function. Understanding this seemingly simple expression opens doors to a broader understanding of polynomial functions and their significance in various fields.
Understanding the Components
The expression 7x³ - 5x² + 3x is a polynomial. More specifically, it's a cubic polynomial because the highest power of the variable x is 3. Let's break down each term:
-
7x³: This is the cubic term. The coefficient is 7, and the variable x is raised to the power of 3. This term dominates the behavior of the polynomial for large values of x.
-
-5x²: This is the quadratic term. The coefficient is -5, and the variable x is squared. This term influences the curve of the polynomial.
-
3x: This is the linear term. The coefficient is 3, and the variable x is raised to the power of 1 (although the '1' isn't explicitly written). This term contributes to the polynomial's slope.
The entire expression is a sum of these individual terms. The absence of a constant term (a term without an x) is noteworthy; it means the graph of this function passes through the origin (0,0).
Algebraic Manipulation: Simplifying and Expanding
While the expression is already in its simplest form, we can explore related scenarios involving simplification and expansion. For example, let's consider scenarios where we might need to:
Factoring the Polynomial
Factoring a cubic polynomial can be challenging. There's no single, guaranteed method like there is for quadratic equations. However, we can try some techniques:
-
Greatest Common Factor (GCF): In this case, the GCF of the terms is x. We can factor it out:
x(7x² - 5x + 3). The resulting quadratic expression within the parentheses might be factorable further, but in this instance, it's not easily factored using integers. -
Rational Root Theorem: This theorem helps identify potential rational roots (roots that are fractions). However, testing the potential rational roots in this case reveals that none are actual roots.
-
Numerical Methods: For more complex polynomials, numerical methods (like the Newton-Raphson method) are often employed to approximate the roots.
Expanding Expressions
Consider a scenario where we need to expand an expression involving our polynomial. For example:
(2x + 1)(7x³ - 5x² + 3x)
This would require using the distributive property (often called FOIL for binomials) to multiply each term in the first expression by each term in the second:
2x(7x³ - 5x² + 3x) + 1(7x³ - 5x² + 3x)
= 14x⁴ - 10x³ + 6x² + 7x³ - 5x² + 3x
= 14x⁴ - 3x³ + x² + 3x
This results in a quartic polynomial (a polynomial of degree 4).
Applications of Cubic Polynomials
Cubic polynomials, like our expression 7x³ - 5x² + 3x, appear in various fields:
Physics and Engineering
-
Projectile Motion: The trajectory of a projectile (like a ball thrown in the air) can be modeled using a quadratic equation, but more complex scenarios, considering factors like air resistance, might involve cubic or higher-order polynomials.
-
Fluid Dynamics: Cubic polynomials can describe the relationship between fluid velocity and pressure under certain conditions.
-
Structural Engineering: The bending of beams and other structural elements can be analyzed using cubic polynomials.
Economics and Finance
-
Cost Functions: The total cost of producing a certain number of goods might be modeled using a cubic polynomial, considering factors like fixed costs, variable costs, and economies of scale.
-
Demand and Supply: While often simplified with linear functions, more complex models of supply and demand might incorporate cubic polynomials.
Computer Graphics and Animation
- Curve Modeling: Cubic Bezier curves, based on cubic polynomials, are widely used in computer graphics and animation to create smooth and aesthetically pleasing curves.
Graphing the Cubic Polynomial
Graphing the function y = 7x³ - 5x² + 3x can provide valuable insights into its behavior. Key features to consider include:
-
x-intercepts (roots): These are the points where the graph intersects the x-axis (where y=0). Finding these roots, as discussed earlier, can be challenging for cubic polynomials.
-
y-intercept: This is the point where the graph intersects the y-axis (where x=0). In our case, the y-intercept is (0,0), as there is no constant term.
-
Turning points: Cubic polynomials can have up to two turning points (local maxima or minima). The exact location of these points can be found using calculus (finding the derivative and setting it to zero).
-
End behavior: As x approaches positive infinity, y approaches positive infinity. As x approaches negative infinity, y approaches negative infinity. This is typical of odd-degree polynomials.
Using graphing software or a graphing calculator allows for a visual representation, revealing the shape and behavior of the polynomial.
Solving Equations Involving the Polynomial
Let's explore how to solve an equation involving our cubic polynomial. Suppose we want to solve:
7x³ - 5x² + 3x = 10
To solve this, we need to rearrange the equation into the standard form of a cubic equation:
7x³ - 5x² + 3x - 10 = 0
As mentioned earlier, solving cubic equations can be challenging. While there are formulas for finding the roots of cubic equations (similar to the quadratic formula, but considerably more complex), numerical methods are often more practical for solving such equations, particularly when exact solutions aren't required.
Conclusion
The seemingly simple mathematical expression 7x³ - 5x² + 3x serves as a gateway to understanding the broader world of polynomial functions. By analyzing its components, exploring algebraic manipulations, appreciating its applications in various fields, and visualizing its graph, we can gain a deeper understanding of its significance in mathematics and its practical relevance across numerous disciplines. While finding exact solutions for cubic equations might require advanced techniques, understanding the fundamental properties and behavior of these polynomials remains crucial for anyone working with mathematical models in diverse fields of study and application.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7x 3 - 5x 2 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.