75 Is What Percent Of 125
News Leon
May 04, 2025 · 4 min read
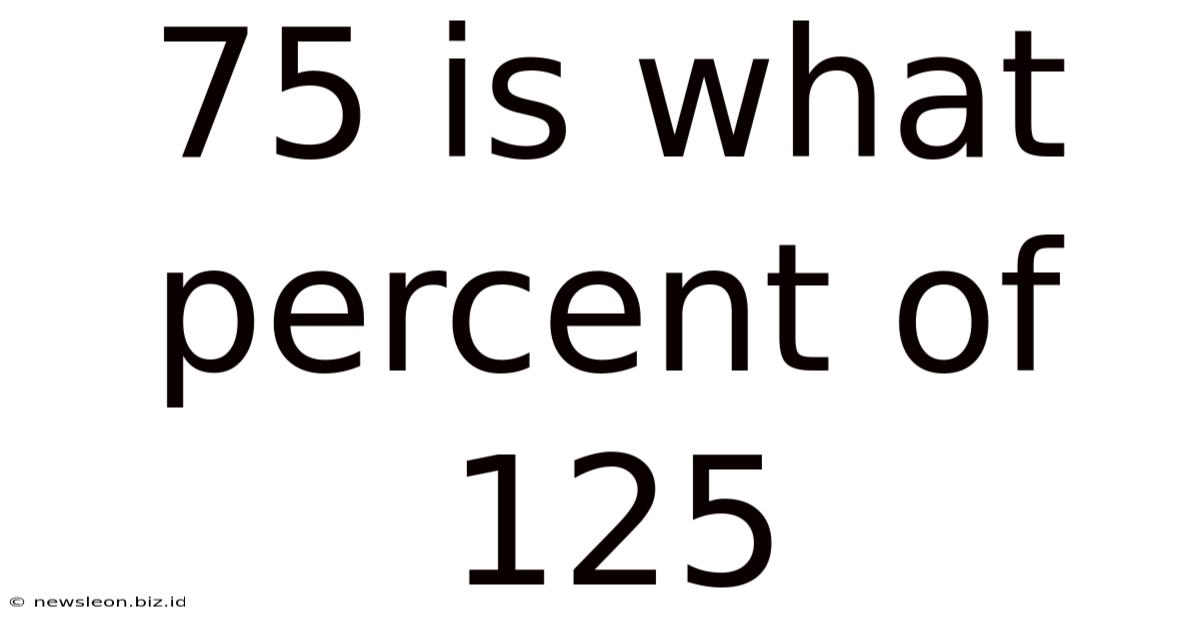
Table of Contents
75 is What Percent of 125? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various fields, from everyday finances to complex scientific analyses. Understanding how to determine what percentage one number represents of another is crucial for interpreting data, making informed decisions, and solving a multitude of practical problems. This comprehensive guide will delve into the calculation of "75 is what percent of 125?", exploring different approaches, providing detailed explanations, and offering valuable insights into the broader concept of percentages.
Understanding Percentages
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Proportion Method
The proportion method is a classic and intuitive approach to solving percentage problems. It leverages the concept of equivalent ratios. We can set up a proportion to represent the problem:
75/125 = x/100
Where:
- 75 represents the part.
- 125 represents the whole.
- x represents the unknown percentage.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
75 * 100 = 125 * x
7500 = 125x
Now, divide both sides by 125:
x = 7500 / 125
x = 60
Therefore, 75 is 60% of 125.
Method 2: Using the Decimal Method
The decimal method offers a more direct approach. We can convert the fraction 75/125 into a decimal by performing the division:
75 ÷ 125 = 0.6
To express this decimal as a percentage, we multiply by 100:
0.6 * 100 = 60%
This confirms our earlier result: 75 is 60% of 125.
Method 3: Using the Formula Method
A more formalized approach involves using the percentage formula:
Percentage = (Part / Whole) * 100%
In our case:
Percentage = (75 / 125) * 100%
Percentage = 0.6 * 100%
Percentage = 60%
This formula provides a structured and efficient way to calculate percentages in various scenarios.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world applications. Consider these examples:
1. Financial Calculations:
- Interest rates: Calculating simple or compound interest on loans or investments involves percentage calculations.
- Discounts and sales tax: Determining the final price of an item after a discount or adding sales tax requires understanding percentages.
- Profit margins: Businesses use percentages to calculate profit margins and assess their financial performance.
2. Data Analysis and Interpretation:
- Statistical analysis: Percentages are crucial in representing data proportions and trends in various statistical analyses.
- Survey results: Presenting survey results often involves expressing responses as percentages of the total sample size.
- Market research: Understanding market share and consumer behavior often relies on percentage calculations.
3. Everyday Life:
- Tip calculations: Determining an appropriate tip in a restaurant requires calculating a percentage of the bill.
- Recipe scaling: Adjusting recipe quantities involves using percentages to scale ingredients up or down.
- Grade calculations: Many academic grading systems utilize percentages to represent student performance.
Expanding on Percentage Concepts: Beyond the Basics
Understanding the fundamentals of percentage calculations opens the door to more advanced concepts:
1. Percentage Increase and Decrease:
Calculating the percentage increase or decrease between two values involves finding the difference between them, dividing by the original value, and multiplying by 100%.
Percentage Change = [(New Value - Original Value) / Original Value] * 100%
2. Percentage Points:
Percentage points represent the arithmetic difference between two percentages. It's crucial to distinguish between a percentage change and a percentage point change. For example, an increase from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself.
3. Compounding Percentages:
Compounding involves applying a percentage change repeatedly over time. This is common in financial calculations involving compound interest.
Troubleshooting Common Errors in Percentage Calculations
Several common errors can occur when calculating percentages:
- Incorrect order of operations: Ensure you follow the order of operations (PEMDAS/BODMAS) correctly, especially when dealing with multiple operations.
- Misinterpreting the "whole": Clearly identify the "whole" or base value upon which the percentage is calculated.
- Confusing percentage change with percentage points: Remember the difference between these two concepts.
- Rounding errors: Be mindful of rounding errors, especially in complex calculations.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a versatile and essential skill applicable across numerous domains. Understanding the various methods – proportion, decimal, and formula – empowers you to solve percentage problems efficiently and accurately. By grasping the fundamental concepts and avoiding common pitfalls, you can confidently apply percentage calculations to interpret data, analyze financial situations, and tackle everyday challenges requiring precise numerical understanding. The simple problem of "75 is what percent of 125?" serves as a springboard to understanding a far broader and more useful mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about 75 Is What Percent Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.