5 Is Multiplied By The Cube Of A Number.
News Leon
Apr 07, 2025 · 5 min read
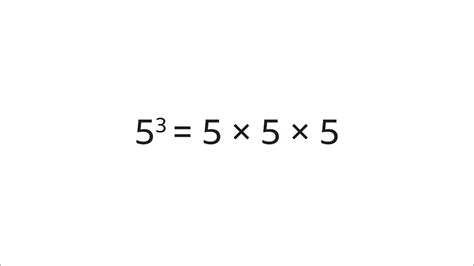
Table of Contents
5 Multiplied by the Cube of a Number: Exploring Mathematical Concepts and Applications
The seemingly simple phrase "5 multiplied by the cube of a number" opens a door to a vast world of mathematical exploration. This seemingly basic operation touches upon fundamental algebraic concepts, has practical applications in various fields, and provides a fertile ground for exploring more advanced mathematical ideas. This article delves into the intricacies of this operation, exploring its mathematical underpinnings, real-world examples, and its potential for further mathematical investigation.
Understanding the Fundamentals: Cubes and Multiplication
Before diving into the complexities, let's solidify our understanding of the core components: cubing a number and multiplication.
What is a Cube?
Cubing a number means raising it to the power of three. In simpler terms, it's multiplying the number by itself three times. For example:
- The cube of 2 (written as 2³) is 2 x 2 x 2 = 8
- The cube of 5 (written as 5³) is 5 x 5 x 5 = 125
- The cube of x (written as x³) is x x x x x = x³
This concept extends to all real numbers, including negative numbers and fractions. Remember that the cube of a negative number will remain negative (a negative multiplied by a negative results in a positive, and then multiplying by another negative returns to a negative).
Multiplication: The Foundation of Arithmetic
Multiplication is a fundamental arithmetic operation that represents repeated addition. When we say "5 multiplied by the cube of a number," we are indicating that the result of cubing the number is then multiplied by 5.
Expressing the Operation Algebraically
To represent "5 multiplied by the cube of a number" algebraically, we use variables. Let's use 'x' to represent the number. The algebraic expression becomes:
5x³
This concise expression captures the entire operation. It's crucial to understand the order of operations (PEMDAS/BODMAS): we cube 'x' first, then multiply the result by 5.
Exploring Different Number Types
Let's explore how the expression 5x³ behaves with different types of numbers:
Positive Integers:
If x = 2, then 5x³ = 5(2³) = 5(8) = 40 If x = 3, then 5x³ = 5(3³) = 5(27) = 135 If x = 10, then 5x³ = 5(10³) = 5(1000) = 5000
As you can see, the output increases rapidly as x increases. This rapid growth is characteristic of cubic functions.
Negative Integers:
If x = -2, then 5x³ = 5(-2)³ = 5(-8) = -40 If x = -3, then 5x³ = 5(-3)³ = 5(-27) = -135 If x = -10, then 5x³ = 5(-10)³ = 5(-1000) = -5000
The results are negative, mirroring the negative input value. The magnitude of the output still increases rapidly with the absolute value of x.
Fractions and Decimals:
If x = 0.5, then 5x³ = 5(0.5)³ = 5(0.125) = 0.625 If x = 1/3, then 5x³ = 5(1/3)³ = 5(1/27) = 5/27 ≈ 0.185
The results are smaller, reflecting the smaller input values.
Zero:
If x = 0, then 5x³ = 5(0)³ = 5(0) = 0
This is a straightforward case where the output is zero.
Graphical Representation: Visualizing the Cubic Function
The expression 5x³ represents a cubic function. Graphing this function provides a visual representation of its behavior. The graph will show a curve that passes through the origin (0,0) and extends infinitely in both the positive and negative x and y directions. The steepness of the curve demonstrates the rapid increase in the output as the input value increases or decreases.
Real-World Applications: Where 5x³ Comes into Play
While seemingly abstract, the concept of "5 multiplied by the cube of a number" has practical applications in various fields:
Volume Calculations:
The volume of a cube is side³. If we have a cube where each side is increased by a factor of x, and we're interested in the volume of another object that is five times this cube, the formula becomes 5x³. This could apply in various fields, such as architecture, engineering, and packaging.
Physics and Engineering:
Many physics equations involve cubic relationships. For example, the power dissipated in a resistor is proportional to the cube of the current. The equation could be modified to include a constant factor like 5 depending on the specific scenario.
Chemistry and Biology:
Certain chemical reactions and biological processes follow cubic relationships. The constant factor of 5 could represent a specific reaction rate or biological factor.
Economics and Finance:
While less common, some economic models might utilize cubic functions to model certain relationships between variables, where the constant 5 would represent a specific economic parameter.
Expanding the Concept: Variations and Extensions
The core concept can be extended in numerous ways:
- Adding a constant: The expression could become 5x³ + c, where 'c' is a constant. This adds a vertical shift to the graph.
- Adding a linear term: The expression could become 5x³ + bx + c, creating a more complex polynomial function.
- Introducing other operations: We could explore expressions like 5x³ + 2x² - 4x + 1, exponentiating the entire expression (e.g., (5x³)²) or exploring composite functions.
Advanced Mathematical Explorations: Derivatives and Integrals
For those with a stronger mathematical background, exploring the derivative and integral of 5x³ opens avenues to calculus and its applications.
- Derivative: The derivative of 5x³ is 15x², representing the instantaneous rate of change of the function.
- Integral: The indefinite integral of 5x³ is (5/4)x⁴ + C, where C is the constant of integration. This represents the area under the curve of the function.
These concepts have wide-ranging applications in optimization, modeling dynamic systems, and other advanced mathematical analyses.
Conclusion: A Foundation for Further Learning
The seemingly simple expression "5 multiplied by the cube of a number" serves as a gateway to a deeper understanding of algebra, functions, and their applications. From its fundamental algebraic representation to its practical uses in various fields and its potential for more advanced mathematical exploration, this concept holds significant value for students and professionals alike. This detailed exploration encourages further investigation into related mathematical concepts, fostering a stronger appreciation for the power and elegance of mathematics. By understanding the nuances of this expression, we equip ourselves with tools to tackle more complex mathematical problems and real-world challenges. The journey of mathematical understanding is ongoing, and this exploration provides a solid foundation for further learning and discovery.
Latest Posts
Latest Posts
-
Square Root Of X 2 X 4
Apr 09, 2025
-
An Electrochemical Cell Is Constructed With An Open Switch
Apr 09, 2025
-
Simplify The Square Root Of 162
Apr 09, 2025
-
Does Amoeba Have A Cell Wall
Apr 09, 2025
-
What Are The Main Functions Of The Operating System
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about 5 Is Multiplied By The Cube Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.