48 Is 12 Of What Number
News Leon
May 03, 2025 · 4 min read
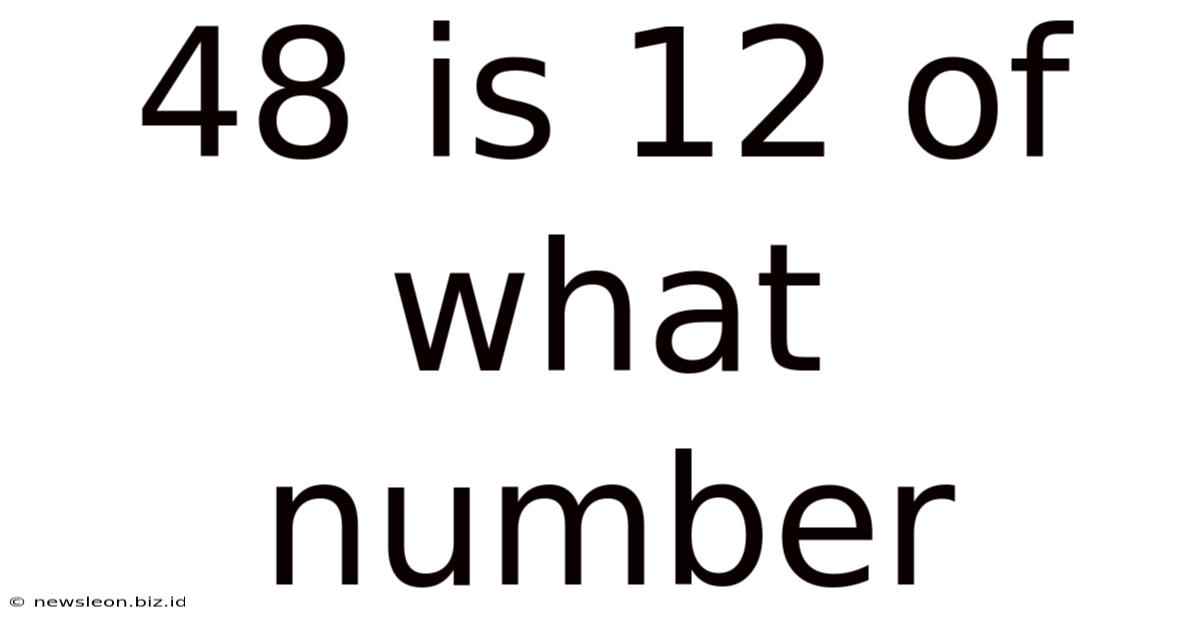
Table of Contents
48 is 12% of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill with applications across numerous fields, from finance and budgeting to scientific analysis and everyday decision-making. Understanding how to calculate percentages efficiently and accurately is crucial. This article delves deep into the question, "48 is 12% of what number?" We'll explore multiple methods to solve this problem, clarifying the underlying concepts and providing practical examples to reinforce your understanding. We'll also discuss the broader context of percentage calculations and their importance.
Understanding Percentages: A Foundation
Before we tackle the specific problem, let's establish a solid understanding of percentages. A percentage represents a fraction of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental relationship is key to solving percentage problems.
Key Terminology
- Percentage: A fraction or ratio expressed as a number out of 100.
- Base: The total amount or whole quantity.
- Part: A portion of the base, representing a percentage of the whole.
- Rate: The percentage expressed as a decimal or fraction.
Method 1: Using the Percentage Formula
The most common method for solving percentage problems involves using the basic percentage formula:
Part = Rate × Base
In our problem, "48 is 12% of what number?", we know the following:
- Part: 48
- Rate: 12% = 0.12 (To convert a percentage to a decimal, divide by 100)
- Base: This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
48 = 0.12 × x
To solve for x, we divide both sides of the equation by 0.12:
x = 48 / 0.12
x = 400
Therefore, 48 is 12% of 400.
Method 2: Setting up a Proportion
Another effective approach to solving percentage problems is by setting up a proportion. A proportion expresses the equality of two ratios. We can represent the problem as:
48/x = 12/100
This proportion states that the ratio of the part (48) to the whole (x) is equal to the ratio of the percentage (12) to 100.
To solve for x, we can cross-multiply:
48 × 100 = 12 × x
4800 = 12x
x = 4800 / 12
x = 400
Again, we arrive at the solution: 48 is 12% of 400.
Method 3: Using the concept of unitary method
The unitary method focuses on finding the value of one unit and then scaling it up to find the required value.
If 12% represents 48, then 1% represents 48/12 = 4.
Therefore, 100% (the whole number) is 4 * 100 = 400.
Hence, 48 is 12% of 400.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining sale prices, markups, and discounts.
- Science: Analyzing data, calculating statistical probabilities, and expressing experimental results.
- Everyday Life: Understanding tips, calculating percentages of ingredients in recipes, and comparing prices.
Beyond the Basic Percentage Calculation: Advanced Concepts
While the problem "48 is 12% of what number?" illustrates a fundamental percentage calculation, understanding percentages involves more advanced concepts:
- Percentage Increase and Decrease: These calculations determine the percentage change between two values. For example, finding the percentage increase in sales from one year to another.
- Compound Interest: This calculates interest on both the principal and accumulated interest.
- Percentage Points: These represent the absolute difference between two percentages, not a relative change.
Tips for Solving Percentage Problems Effectively
- Clearly identify the known and unknown values: This helps you structure the problem correctly.
- Use consistent units: Ensure that all values are expressed in the same units.
- Convert percentages to decimals or fractions: This simplifies the calculations.
- Double-check your work: Ensure your answer is logical and reasonable within the context of the problem.
- Practice Regularly: The more you practice, the more confident and efficient you'll become in solving percentage problems.
Conclusion
Solving the problem "48 is 12% of what number?" effectively demonstrates the fundamental principles of percentage calculations. By mastering these principles and applying various methods—such as using the percentage formula, setting up proportions, or employing the unitary method—you can confidently tackle a wide range of percentage-related problems across various disciplines and everyday scenarios. Remember the importance of understanding the underlying concepts and practicing regularly to develop proficiency in this essential mathematical skill. The ability to work with percentages is a powerful tool that enhances your analytical skills and helps you make informed decisions in various aspects of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about 48 Is 12 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.