3 More Than Twice A Number
News Leon
Apr 06, 2025 · 4 min read
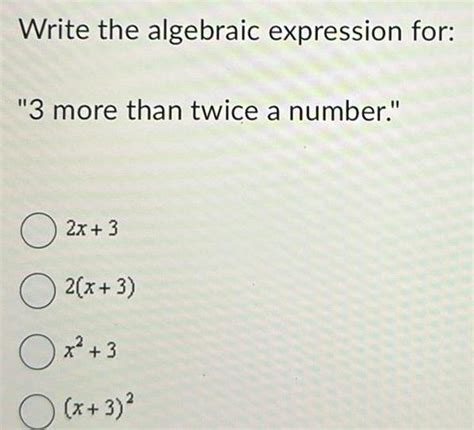
Table of Contents
3 More Than Twice a Number: Exploring Mathematical Concepts and Real-World Applications
The seemingly simple phrase "3 more than twice a number" hides a wealth of mathematical concepts and practical applications. This seemingly basic algebraic expression opens doors to understanding fundamental principles, solving complex problems, and even appreciating the elegance of mathematical modeling in diverse fields. Let's delve deep into this expression, uncovering its intricacies and showcasing its relevance in the real world.
Understanding the Algebraic Representation
The phrase "3 more than twice a number" translates directly into an algebraic expression. Let's break it down step-by-step:
- A number: We represent this unknown number with a variable, typically 'x'.
- Twice a number: This means multiplying the number by 2, resulting in 2x.
- 3 more than twice a number: This indicates adding 3 to the result, giving us the final expression: 2x + 3.
This simple expression forms the foundation for numerous mathematical explorations and problem-solving scenarios.
Solving Equations Involving "3 More Than Twice a Number"
The true power of this expression lies in its use within equations. Let's consider some examples:
Example 1: Finding the Number
Problem: "3 more than twice a number is 11. Find the number."
Solution:
- Translate the problem into an equation: 2x + 3 = 11
- Solve for x:
- Subtract 3 from both sides: 2x = 8
- Divide both sides by 2: x = 4
Therefore, the number is 4.
Example 2: A More Complex Scenario
Problem: "Twice a number, increased by 3, is equal to the number itself plus 15. Find the number."
Solution:
- Translate the problem into an equation: 2x + 3 = x + 15
- Solve for x:
- Subtract x from both sides: x + 3 = 15
- Subtract 3 from both sides: x = 12
Therefore, the number is 12.
Example 3: Inequalities
The expression can also be used in inequalities. For example:
Problem: "3 more than twice a number is greater than 17. Find the range of possible values for the number."
Solution:
- Translate the problem into an inequality: 2x + 3 > 17
- Solve for x:
- Subtract 3 from both sides: 2x > 14
- Divide both sides by 2: x > 7
Therefore, the number is greater than 7.
Real-World Applications: Beyond the Classroom
While seemingly abstract, the concept of "3 more than twice a number" finds practical applications in various real-world situations:
1. Geometry and Measurement
Imagine calculating the perimeter of a rectangle where the length is 3 units more than twice its width. If the width is represented by 'x', the length would be 2x + 3. This expression allows us to formulate equations to find the dimensions given the perimeter.
2. Financial Calculations
Consider a scenario where you earn a base salary plus commission. Let's say your commission is twice the number of units sold, plus a $3 bonus. The total earnings can be represented by 2x + 3, where 'x' is the number of units sold. This helps in calculating potential earnings based on sales projections.
3. Physics and Engineering
Many physics equations involve linear relationships similar to "2x + 3." For instance, calculating the total distance traveled by an object with initial velocity and constant acceleration could involve a similar structure.
4. Data Analysis and Modeling
In data analysis, this expression could represent a simple linear model. For example, if 'x' represents the number of advertising dollars spent, and '2x + 3' represents the resulting profit, this allows analysts to create projections and understand the relationship between spending and returns.
Expanding the Concept: More Complex Scenarios
The core principle of "3 more than twice a number" can be extended to more complex algebraic expressions. Consider:
1. Multiple Variables:
Imagine a scenario with two numbers, 'x' and 'y'. We could express "3 more than twice the sum of two numbers" as 2(x + y) + 3. This adds another layer of complexity, requiring simultaneous equations to solve for both unknowns.
2. Higher-Order Polynomials:
We can integrate "2x + 3" into higher-order polynomial expressions. For example, (2x + 3)² expands to 4x² + 12x + 9, showcasing how a simple expression can contribute to more complex mathematical models.
3. Functions and Graphs:
Representing "2x + 3" as a function, f(x) = 2x + 3, allows us to visualize its behavior graphically. This provides a clear visual representation of the linear relationship between x and f(x), allowing for insights into the function's slope, intercept, and overall behavior.
Conclusion: The Enduring Relevance of Simple Expressions
The seemingly simple expression "3 more than twice a number" provides a powerful foundation for understanding fundamental algebraic concepts, solving problems, and applying mathematical principles to real-world situations. From basic equation solving to complex modeling in various fields, this expression demonstrates the elegance and practical utility of even the most elementary mathematical tools. Its enduring relevance lies in its ability to build a strong foundation for tackling more complex mathematical challenges, highlighting the interconnectedness of seemingly simple concepts within the broader mathematical landscape. By exploring this expression in depth, we gain a deeper appreciation for the beauty and power of mathematics in our everyday lives.
Latest Posts
Latest Posts
-
An Oxidizing Agent Is A Substance That
Apr 08, 2025
-
A Rectangle Has How Many Lines Of Symmetry
Apr 08, 2025
-
Is Electric Field Scalar Or Vector
Apr 08, 2025
-
Which Of The Following Statements Is True Of Research Samples
Apr 08, 2025
-
Which Of The Following Was A Function Of Settlement Houses
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about 3 More Than Twice A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.