3 Is To 8 As X Is To 32
News Leon
Apr 20, 2025 · 5 min read
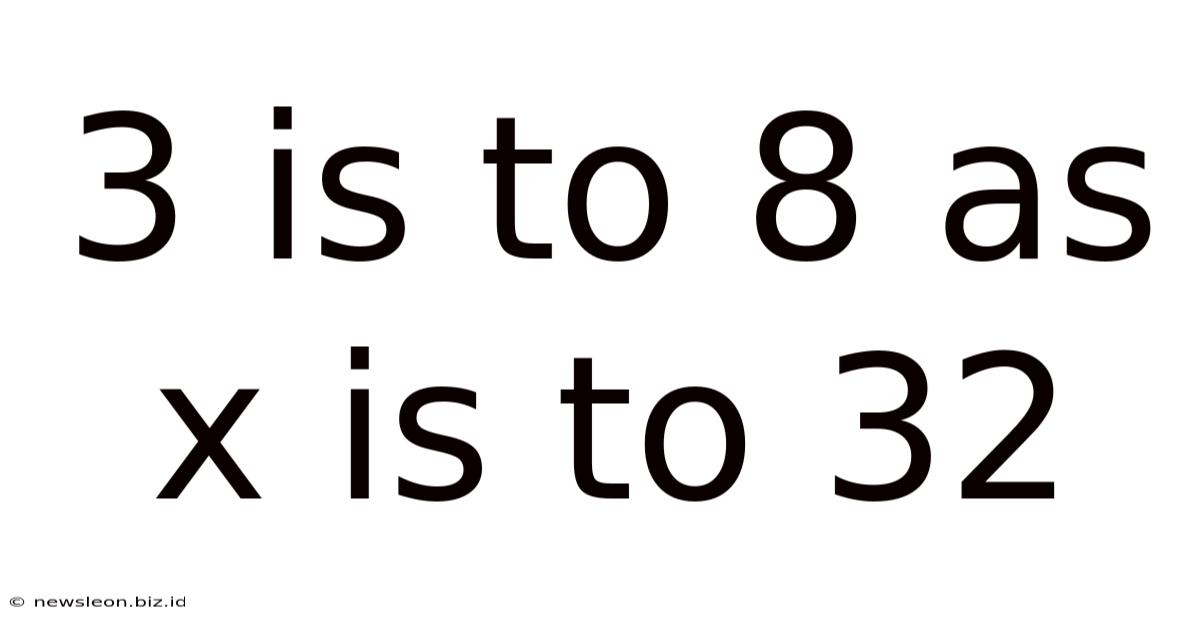
Table of Contents
3 is to 8 as x is to 32: Unlocking the Power of Proportions
Solving mathematical proportions might seem like a dry, academic exercise, but the ability to understand and solve these problems is a powerful tool with far-reaching applications in numerous fields. From scaling recipes in the kitchen to calculating the dimensions of architectural models and even predicting market trends in finance, the concept of proportion underpins a vast array of real-world situations. This article delves deep into the seemingly simple equation "3 is to 8 as x is to 32," exploring different approaches to solving it and highlighting the broader significance of proportional reasoning.
Understanding Proportions: A Foundation in Ratios
Before we tackle the specific problem, let's establish a firm grasp of what proportions are. A proportion is simply a statement that two ratios are equal. A ratio is a comparison of two quantities. We often express ratios using colons (e.g., 3:8) or as fractions (e.g., 3/8).
In our example, "3 is to 8 as x is to 32," we have two ratios: 3/8 and x/32. The statement implies that these two ratios are equal:
3/8 = x/32
This equation represents a proportion, and our task is to find the value of x that makes the equation true.
Methods for Solving Proportions: A Multifaceted Approach
Several methods exist for solving proportions. Let's explore the most common and effective ones, applying them to our specific problem:
1. The Cross-Multiplication Method: A Classic Technique
This is perhaps the most widely known and straightforward method. Cross-multiplication involves multiplying the numerator of one ratio by the denominator of the other and setting the products equal to each other. In our case:
3 * 32 = 8 * x
This simplifies to:
96 = 8x
Now, we can solve for x by dividing both sides of the equation by 8:
x = 96 / 8
x = 12
Therefore, the solution to the proportion is x = 12.
2. Finding the Scale Factor: A Conceptual Approach
This method focuses on understanding the relationship between the two ratios. We can determine the scale factor by dividing the second term of one ratio by the corresponding term in the other ratio. In our problem:
32 / 8 = 4
This tells us that the second ratio is 4 times larger than the first ratio. To find x, we multiply the first term of the first ratio by the scale factor:
3 * 4 = 12
Again, we arrive at the solution x = 12. This approach is particularly insightful as it reveals the underlying relationship between the quantities.
3. Using Equivalent Fractions: A Visual Representation
This method leverages the fundamental concept that equivalent fractions represent the same value. We can manipulate the given ratio (3/8) to create an equivalent fraction with a denominator of 32. To do this, we ask ourselves: "What do we need to multiply 8 by to get 32?" The answer is 4. Therefore, we must multiply both the numerator and denominator of 3/8 by 4:
(3 * 4) / (8 * 4) = 12/32
Now we have an equivalent fraction, 12/32, which is equal to 3/8. Thus, x = 12.
Beyond the Equation: Real-World Applications of Proportions
While solving "3 is to 8 as x is to 32" might seem like a purely mathematical exercise, the principle of proportions has extensive practical applications across diverse fields:
1. Scaling Recipes: Culinary Proportions
Imagine you have a recipe that calls for 3 cups of flour and 8 cups of water. If you want to make a larger batch using 32 cups of water, you can use proportions to determine the required amount of flour:
3/8 = x/32
Solving this proportion using any of the methods described above, we find that x = 12. Therefore, you need 12 cups of flour for your larger batch.
2. Map Scaling: Geography and Cartography
Maps use proportions to represent vast geographical areas on a smaller scale. If a map's scale is 1:100,000, it means that 1 unit on the map represents 100,000 units in reality. This allows for accurate representation and measurement of distances and areas.
3. Architectural Modeling: Precision in Design
Architects frequently use proportions to create scaled models of buildings. If a model is built at a scale of 1:50, each centimeter in the model represents 50 centimeters in the actual building. This helps in visualizing and refining designs before construction begins.
4. Financial Calculations: Interest and Investments
Proportions play a vital role in financial calculations, such as determining interest earned on investments or calculating loan repayments. Understanding proportions helps in making informed financial decisions.
5. Scientific Experiments: Data Analysis
In scientific experiments, proportions are used to analyze data and draw conclusions. For instance, if a scientist finds that 3 out of 8 samples show a certain characteristic, they can use proportions to predict the likelihood of finding that characteristic in a larger sample.
Advanced Applications and Related Concepts
The concept of proportions extends beyond simple algebraic equations. It forms the basis of more advanced mathematical concepts, including:
- Similar Triangles: In geometry, similar triangles have corresponding angles that are equal and corresponding sides that are proportional. Understanding proportions is crucial for solving problems involving similar triangles.
- Trigonometry: Trigonometric functions (sine, cosine, tangent) are defined as ratios of sides in right-angled triangles, showcasing the deep connection between proportions and trigonometry.
- Linear Equations: Proportions are intimately linked to linear equations, which represent relationships between variables with a constant rate of change.
- Percentage Calculations: Percentages are essentially ratios expressed as a fraction of 100. Understanding proportions is foundational to working with percentages.
Conclusion: Mastering Proportions for a Brighter Future
The seemingly simple equation "3 is to 8 as x is to 32" unlocks a world of mathematical understanding and practical applications. Mastering the art of solving proportions is not merely an academic exercise; it's a valuable skill applicable across numerous fields. By understanding the different methods of solving proportions and recognizing their pervasive presence in our daily lives, we can enhance our problem-solving abilities and navigate the complexities of the world around us with greater confidence and competence. The ability to think proportionally empowers us to scale recipes, interpret maps, design buildings, manage finances, and analyze scientific data—all crucial elements in building a brighter future.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Is To 8 As X Is To 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.